Aufgabe:
1. Bestimmen Sie den größtmöglichen Definitionsbereich der folgenden Funktionen (stellen Sie ihn als Vereinigung von Intervallen dar).
a) \( f(x)=\frac{3}{7-x} \)
b) \( f(x)=\frac{x+7}{x^{2}-4} \)
c) \( f(x)=\frac{x^{2}-1}{x+1} \)
d) \( f(x)=\frac{5\left(x^{2}-1\right)}{x-1} \)
e) \( f(x)=\frac{x(x+1)}{|x|} \)
f) \( f(x)=\frac{1}{\left|x^{3}-1\right|} \)
g) \( f(x)=\frac{x^{2}}{\sqrt{|x-2|}} \)
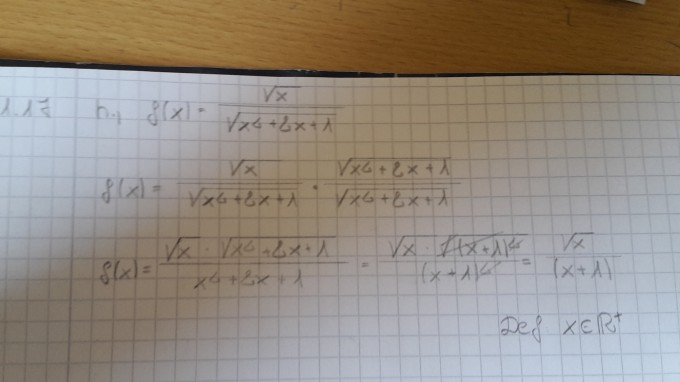
h) \( f(x)=\frac{\sqrt{x}}{\sqrt{x^{2}+2 x+1}} \)
2. Bilden Sie \( f+g, f \cdot g, f-g \) und \( \frac{f}{g} \) und bestimmen Sie den maximalen Definitionsbereich der so entstandenen Funktionen.
Ansatz/Problem:
Ich habe die Angabe und auch meinen Lösungsweg als Bild unten angehängt. Es handelt sich um Beispiel h. In der Vorlesung wurde auf das Thema nicht eingegangen und auch kein Beispiel gerechnet aber in der Übung müssen wir es können und ich steh daher ziemlich auf der Leitung.
Könnte mir vielleicht jemand erklären ob mein Rechengang richtig ist und wenn nicht vielleicht den richtigen Rechengang erläutern?