Aufgabe:
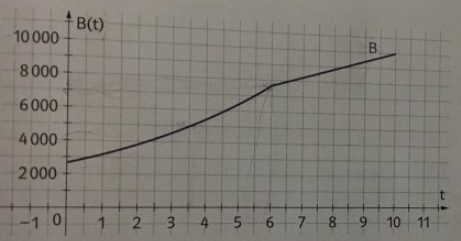
In der Graphik sieht man die Bevölkerungsentwicklung B einer Stadt in Abhängigkeit der seit dem Jahr 2000 vergangenen Jahre (t). In der Tabelle sind genaue Daten zu bestimmten Jahren ablesbar.
| Jahr | Bevölkerung |
| 2001 | 3323 |
| 2003 | 4550 |
| 2006 | 7670 |
| 2008 | 8868 |
a) Erkläre anhand der Daten der Tabelle, warum in den ersten sechs Jahren ein exponentielles Wachstumsmodell angenommen werden kann. Stelle ein Wachstumsgesetz mit Hilfe der Werte von 2001 und 2003 in der Form \( B(t)=a \cdot b^{t} \) dar \( (t \) ist die Anzahl der seit dem Jahr 2000 vergangenen Jahre).
b) Erkläre anhand der Graphik, warum ab 2006 ein lineares Wachstum geeignet ist und stelle ein lineares Wachstumsmodell mit Hilfe der Werte von 2006 und 2008 auf.
Ansatz:
Auf d komme ich indem ich 2008-2006 durch 2 rechne, da kommt 599 heraus. Aber wie komme ich auf k?