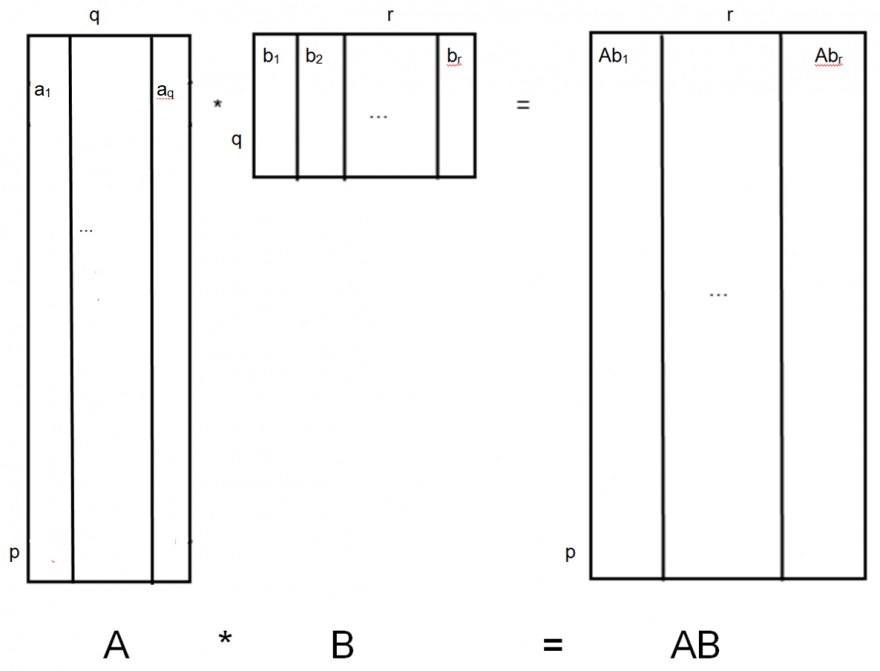
\( \begin{pmatrix} a_{1}\\a_{2}\\...\\a_{p} \end{pmatrix} \) * \( \begin{pmatrix} b_1 & b_2 & ... & b_r \end{pmatrix} \) = \( \begin{pmatrix} Ab_1 & Ab_2 & ... & Ab_r \end{pmatrix} \)
(a) Rang(AB) ≤ Rang(B)
Bew:
Falls eine lin.abhängige Auswahl b1', b2', ... bk' existiert, gilt:
\( \sum\limits_{n'=1'}^{k'}{λ_{n'}b_{n'}} \) = 0 ⇒ ∃λn' ≠0
d.h. \( \sum\limits_{n'=1'}^{k'}{λ_{n'}Ab_{n'}} \) = 0 = A\( \sum\limits_{n'=1'}^{k'}{λ_{n'}b_{n'}} \) ⇒ ∃λn' ≠0
d.h. die Auswahl Ab1', Ab2', ... Abk' ist dann lin.abhängig.
d.h. eine Auswahl lin.unabhängiger Ab's ist höchstens so mächtig wie eine Auswahl lin. unabhängiger b's.
d.h Rang(AB) ≤ Rang(B)
Falls keine lin.abhängige Auswahl b1', b2', ... bk' existiert, gilt: q=r = Rang(B), Rang(AB)≤r und Rang(AB)≤p, also auch
Rang(AB)≤Rang(B) q.e.d.
(b) Rang(AB) ≤ Rang(A)
Bew:
Sei b*= \( \begin{pmatrix} b^{*}_1\\b^{*}_2\\... \\b^{*}_q\end{pmatrix} \) ∈ {b1,b2,...,br}
dann Ab* = \( \sum\limits_{n=1}^{q}{a_{n}b^{*}_{n}} \) liegt als Lin.komb. im Erzeugnis < a1,a2,...,aq >
also liegen alle Ab1,Ab2,...,Abq im Erzeugnis < a1,a2,...,aq >
also dim(<Ab1,Ab2,...,Abq>) = Rang(AB) ≤ dim(< a1,a2,...,aq >) = Rang(A) q.e.d.