Question

Gegeben ist ein Viereck ABCD

AD=52mm CD=87mm α =DAB=81◦, γ =BCD=62◦, δ =CDA=105◦ (a) Berechnen Sie Die Längen der Seiten AB und BC!

(b) Berechnen sie den Flächeninhalt des Vierecks ABCD! 

Answer 1

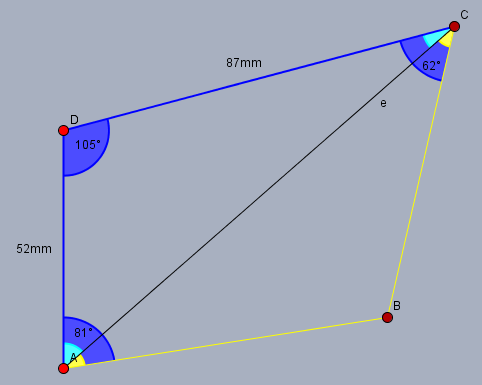
Berechne zunächst die Diagonale \(AC\) mit dem Cosinussatz. Es ist $$AC^2=AD^2+CD^2-2\cdot AD \cdot CD \cdot \cos \delta$$ Dann den Winkel \(DAC\) (hellblau bei A) mit dem Sinussatz $$ \frac{\sin DAC}{DC} = \frac{\sin \delta }{AC} $$ Den Winkel \(ACD\) (hellblau bei C) erhält man aus der Winkelsumme im Dreieck \(ACD\).

Die beiden Winkel \(CAB\) und \(BCA\) (gelb) berechnet man aus den Differenzen $$CAB = \alpha - DAC$$ $$BCA = \gamma - ACD$$ Den Winkel \(\beta\) erhält man aus der Winkelsumme im Viereck $$\beta = 360-\alpha - \gamma - \delta = 112°$$ Mit Hilfe des Sinussatzes lassen sich nun die beiden Seiten \(AB\) und \(BC\) bestimmen. Es ist $$\frac{AB}{\sin BCA}=\frac{AC}{\sin \beta}$$ $$\frac{BC}{\sin CAB}=\frac{AC}{\sin \beta}$$

Die Fläche des Vierecks ist gleich der Summe der Flächen der beiden Dreiecken \(ACD\) und \(ABC\). Da \(AC\) bereits bekannt ist, lassen sich die beiden Flächen mit dem Satz des Heron berechnen.

 Zur Kontrolle: \(AB=70,2\text{mm}\), \(BC=65,2\text{mm}\) und \(F=43,08\text{cm}^2\).

Gruß Werner

Answer 2

Da 3 Winkel gegeben sind, kann man den 4. Winkel β ausrechnen. Die beiden Schenkel dieses Winkels nenne x und y. Die Diagonale AC lässt sich mit dem Kosinussatz bestimmen. Die Diagonale DB sei d. Dreimalige Formulierung des Kosinussatzes (je einmal für den Winkel α, β, und γ) ergibt drei Gleichungen mit drei Unbekannten d, x, y. Vielleicht lässt sich das System lösen?