Hallo ihr lieben.
Erst mal ein frohes neues Jahr.
Icgh hab folgene Aufgabe: (Der wolte meine Formel vom Formeleditor auf patu nicht anzeigen, tut mir leid.)
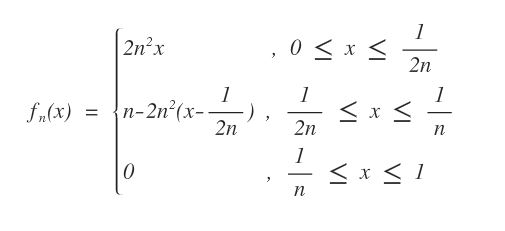
$$ n \in N $$ und $${ f }_{ n }:\left[ 0,1 \right]$$
So zuerst soll ich die Grenzfunktion f der Funktionenfolge f_n sowie $$\lim _{ n\rightarrow \infty }{ \int _{ 0 }^{ 1 }{ { f }_{ n }(x)dx } } $$
Anschließend soll ich noch zeigen, dass $$\lim _{ n\rightarrow \infty }{ \int _{ 0 }^{ 1 }{ { f }_{ n }(x)dx } } \neq \quad \int _{ 0 }^{ 1 }{ f(x) } dx$$
Ich hab leider noch nie wirklich mit Fallunterscheidungen gearbeitet und bin mir daher unschlüssig wie ich die Aufgabe bearbeiten muss.
Ich wäre für jeglichen Hinweise sehr dankbar, da ich irgendwie noch nicht wirklich in dem Arbeitstrott, nach den Feiertagen, drin bin.
Liebe Grüße und vorweg schonmal vielen Dank für die Hilfe!