Grenzwert mit Fallunterscheidung

Question

Aufgabe:

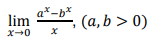
Text erkannt:

\( \lim \limits_{x \rightarrow 0} \frac{a^{x}-b^{x}}{x},(a, b>0) \)

Ich weiß nicht, wie ich diesen Grenzwert zu bestimmen habe. Ich gehe davon aus, dass eine Fallunterscheidung zu tun ist und dass das Ergebnis etwas mit einem Logarithmus zu tun hat. Allerdings weiß ich nicht, was genau ich tun muss.

Vielen Dank schonmal für die Hilfe.

Answer 1

Du musst nur eine 1 dazwischen schieben. Dann hast du den Differenzenquotienten für \(a^x\) und \(b^x\) an der Stelle \(x=0\).

$$\lim \limits_{x \rightarrow 0} \frac{a^{x}-b^{x}}{x} = \lim \limits_{x \rightarrow 0} \left(\frac{a^{x}-1}{x} - \frac{b^{x}-1}{x} \right) = \ln a - \ln b$$

Comments

Ich glaube, dass wir das noch nicht hatten. Geht das auch anders?

---

Ihr hattet noch keine Ableitung?

Ihr müsstet doch zumindest die e-Funktion gehabt haben. Wie wurde die denn bei euch definiert?

Und außerdem müssten dann auch grundlegende Eigenschaften der e-Funktion behandelt worden sein, bevor man euch auf solche Grenzwerte loslässt.

---

Ähm doch, aber ich sehe nicht, wo man das hier anwenden kann. Oder ist das die Regel von l'Hospital?

---

e-Funktion hatten wir auch komplett. Aber ich sehe keinen Zusammenhang dazwischen. ^^

---

Wenn ihr L'Hospital hattet, geht das sogar noch schneller.

$$\lim \limits_{x \rightarrow 0} \frac{a^{x}-b^{x}}{x} \stackrel{L'Hospital}{=} \lim \limits_{x \rightarrow 0}\frac{\ln a \cdot a^{x} - \ln b \cdot b^{x}}{1} = \ln a - \ln b$$

Übrigens: \(a^x = e^{x\ln a}\). Das ist der Zusammenhang zwischen der e-Funktion und \(a^x\).

---

Oh mein Gott, wie hab ich das denn nicht gesehen? xD Tut mir leid und vielen Dank ^^

---

Dann ist die Angabe, dass a,b > 0 gilt nicht dazu da, dass man den ln anwenden kann richtig?