Taylorformel mit Lagrangescher Restgliedabschätzung

Question

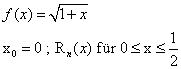
Obenstehende Funktion ist durch eine Taylorformel vom Grad n=3 zu approximieren und eine Fehlerabschätzung vorzunehmen.
R_n(x) muss R₃(x) heißen.

Das Polynom lautet bei mir

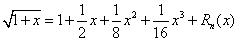
das Restglied

Wenn ich x=1/2 verwende, komme ich auf einen möglichen Fehler von 

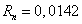
Kann das jemand bestätigen oder mich berichtigen?
Mir geht es vor allem um die Fehlerabschätzung über die Restgliedformel.
Liege ich richtig wenn ich x=1/2 verwende?

Vielen Dank für Eure Mühe.

 
Frank

Comments

ich komme auf gerundet 0,01465... wie sieht denn dein bruch aus?

---

Hallo gollumgollumgirl,

meine Formel sieht so aus:

und das korrigierte Ergebnis so:

Hast Du eventuell noch Hinweise/Verbesserungen?

Frank

---

damit komme ich auf gerundet 0,000610352 bzw.  6,10352e-04

du hast ja x₀ = 0 , 0 ≤ x ≤ 1/2 

Und nun gibt es ein unbekanntes ξ dass zwischen x₀ und x liegt: 0 ≤ ξ ≤ 1/2

du musst also in ξ und x trennen und jeweils zur abschätzung behandeln

---

Hallo gollumgollumgirl,

jetzt wird es interessant und ich bin hellwach.
Für mich ist doch

Und x bewegt sich zwischen 0 und 1/2.
Also setze ich für x jenen Betrag ein, welcher den Term 
 
maximiert. Und das ist 1/2.

Sehe ich das falsch?
Wenn ja, korrigier mich bitte. Wie ist es richtig?

Frank

---

ich glaube du hast das mit f⁽⁴⁾ (ξ) falsch verstanden. du hast benutzt: f⁽⁴⁾ (x) 

---

Hallo gollumgollumgirl,

vielen Dank für Deine Hilfe.

Frank

Answer 1

Die Formel lautet aber $$R_3(x)=\frac{f^{(4)}(\xi)}{4!}x^4\quad\text{mit $\xi\in(0,x)$.}$$

Du hast aus dem ξ einfach ein x gemacht und die 4! weggelassen. Da wird's wohl nicht stimmen.

Comments

Hallo Fakename,

danke für Deinen Hinweis.

Wenn ich es korrekt einsetze, sieht es so aus:

Wenn ich für x=1/2 einsetze, komme ich auf 

Ist damit meine Fehlerabschätzung zutreffend?

 
Frank

---

Zumindest mir kannst Du weiterhin kein x für ein ξ vormachen. Solange Du das tust, ist Dein Resultat falsch. Auch kannst Du den Rest nicht ausrechnen, sondern bloss abschaetzen. Also nix  R₃(x) = ... Das Ergebnis wird z.B. die Form |R₃(x)| < {passende Zahl} haben.

---

Hallo Fakename,

vielen Dank für Deine Hilfe.

Frank