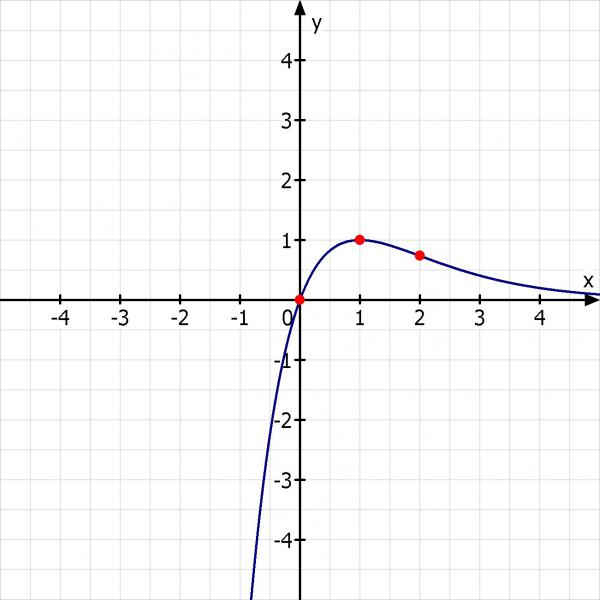
Die Funktion und Ableitungen
f(x) = x·e^{1 - x}
f'(x) = e^{1 - x}·(1 - x)
f''(x) = e^{1 - x}·(x - 2)
f''(x) = e^{1 - x}·(3 - x)
Y-Achsenabschnitt
f(0) = 0
Nullstellen f(x) = 0
x·e^{1 - x} = 0 | Satz vom Nullprodukt. Da die e-Funktion nicht 0 werden kann muss x = 0 sein
x = 0
Extremstellen f'(x) = 0
e^{1 - x}·(1 - x) = 0 | Satz vom Nullprodukt. e-Funktion kann nicht null werden.
1 - x = 0
x = 1
f''(1) = -1 --> Hochpunkt
f(1) = 1 --> HP(1 | 1)
Wendestellen f''(x) = 0
e^{1 - x}·(x - 2) = 0
x - 2 = 0
x = 2
f''(2) <> 0
f(2) = 2/e = 0.7358 --> WP(2 | 0.7358)
Skizze