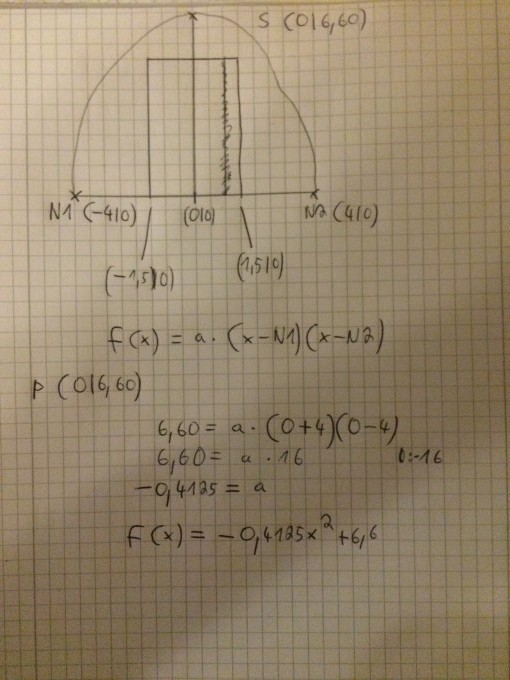Parabel in Form einer Brücke berechenen (Realsituation)

Question

Natürlich gibt es in meinem Mathe Buch keine Lösungen zu den Aufgaben, deshalb bin ich mir nicht sicher ob mein Ansatz nun richtig ist.

Die Aufgabenstellung lautet:

Eine Brückendurchfahrt ist 6,6m hoch und 8m breit.

Ein Fahrzeug ist 3m breit und 4,80m hoch.

Kann dieses Fahrzeug unter der Brücke hindurchfahren?

Hier ist mein Rechenweg, ich bin soweit gekommen das ich die Parabel der Brücke habe, doch wie fahre ich nun fort, vorausgesetzt meine Rechnung ist überhaupt richtig?

 

Answer 1

Deine Funktionsgleichung für die parabel ist richtig. Die frage ist nun, darf der Lkw in der Mitte der Straße fahren oder muss er nicht vielmehr auf "seiner seite" bleiben? In deiner skizze fährt er in der Mitte. 

Comments

Also ich gehe davon aus dass das Fahrzeug mittig unter der Brücke durchfährt, was wäre ihr Lösungsansatz?

---

Ich würde wie unten schon mal dargestellt, den Funktionswert an der Stelle 1,5 berechnen. Da kommt 5,67 raus. Da das mehr 4,8m ist, passt der Lkw hindurch.

---

Vielen Dank für ihre Hilfe komme nun auch auf das Ergebnis, hatte ihre Antwort eben übersehen.

---

Sehr gerne. Du kannst ruhig auch du sagen. Hier im Forum duzen sich alle weil man eh nicht weiß wer wie alt ist.

Answer 2

Deine Parabelfunktion ist korrekt.
f ( x ) = - 6.6 / 16 * x + 6.6

Du berechnest den Funktionswert ( Höhe )
der Parabel an der Stelle der Außenkante
des LKW.

Mittig fahrend
f ( 1.5 ) =- 6.6 / 16 * 1.5 + 6.6 = 5.98 m

Auf einer Fahrbahnseite fahrend
f ( 3 ) = - 6.6 / 16 * 3 + 6.6 = 5.36 m

Der LKW mit einer Höhe von  4.80 m
passt in beiden Fällen durch den Tunnel

Comments

Vielen dank schonmal, ja der LKW soll in der Mitte fahren.

Ich komme grade nicht mehr dahinter in welche formel dies eingesetzt wurde?

Könnte sie sie kurz mit den Variablen auschreiben?

Mittig fahrend 
f ( 1.5 ) =- 6.6 / 16 * 1.5 + 6.6 = 5.98 m

f(x) = a * ? + c  

---

Das liegt daran dass es nicht stimmt.

f (1,5)=-0,4125*(1,5)^2+6,6=-0,4125*2,25+6,6=5,67

---

Fehlerkorrektur

Parabelfunktion
f ( x ) = - 6.6 / 16 * x ^2 + 6.6

Mittig fahrend
f ( 1.5 ) =- 6.6 / 16 * 1.5^2 + 6.6 = 5.67 m

Auf einer Fahrbahnseite fahrend
f ( 3 ) = - 6.6 / 16 * 3^2 + 6.6 = 2.89 m

Mittig fahrend passt der LKW unter der
Brücke durch.