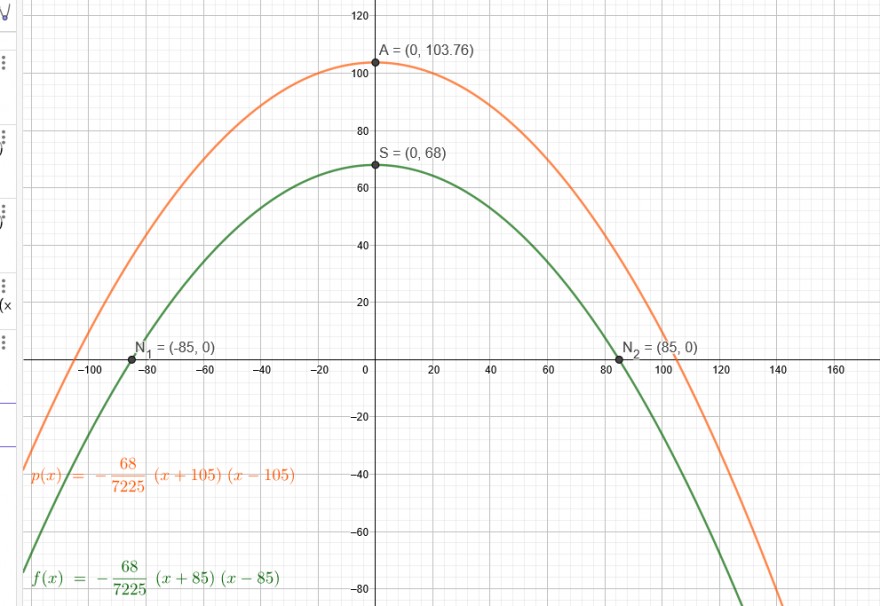
Es gibt da eine Brücke die wie eine Parabel fungiert. Die innere höhe ist gegeben diese liegt bei 68m und die Breite vom linken Fußpunkt bis rechten Fußpunkt sind 170m. Ich soll nun die innere Höhe berechnen, wenn der Brückenbogen in einem horizontalen abstand von 20m abstand von den Fußpunkten liegt. Quasi statt 170m gelten jetzt 20m, das wird logischerweise in der Parabelförmigen Brücke weiter oben sein müssen
1.Parabel:
f(x)=a*(x-N₁)*(x-N₂)
N₁(-85|0) und N₂(85|0)
f(x)=a*(x+85)*(x-85)
Scheitelpunkt: S(0|68)
f(0)=a*(0+85)*(0-85)=-7225a
-7225a=68 a=-\( \frac{68}{7225} \)
f(x)=-\( \frac{68}{7225} \)*(x+85)*(x-85)
veränderte Parabel:
p(x)=-\( \frac{68}{7225} \)*(x+85+20)*(x-85-20)= -\( \frac{68}{7225} \)*(x+105)*(x-105)
Innere Höhe:
p(0)= -\( \frac{68}{7225} \)*(0+105)*(0-105)=\( \frac{68}{7225} \)*\( 105^{2} \)= \( \frac{1764}{17} \)≈103,76m