Hi !
Kurze Skizze : 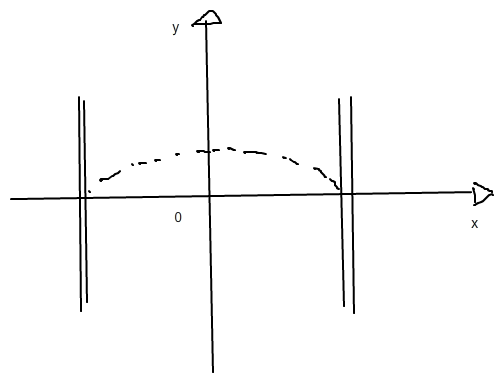
Funktion 2.Grad ! Alarmglocke ! 3.Gleichungssysteme notwendig
f(x)=ax2 +bx + c
Dafür suchen wir jetzt a, b und c.
Wir wissen : 254m hohen Pfeil der der Store Baelt-Brücke in Dänemark beträgt 1624m
Die Punkte sind genau gleich entfernt. Der Mittelpunkt ist der 0-Punkt im Koordinatensystem, daher haben wir einmal den Punkt (-812|254) und (+812|254) Wir haben schon mal 2 Infos, nicht schlecht !
Die Durchfahrtshöhe der Brücke beträgt 65m. Stell dir eine Hängebrücke vor, die nach oben gebogen st, dort ist der Hochpunkt .
Also ist bei ( 0| 65 ) ein Extrema !
Zusammen sieht das dann so aus
f(-812) = 254
f(812) = 254
f(0) = 65 oder f'(0)= 0
Nun setzt du diese Punkte in x von f(x)=ax2 +bx + c
f(65)=ax2 +bx + c = 4225a + 65b + c = 65 ( b ist 0 siehe unten )
f(65)= 4225a + c = 65
Bilden wir mal die Ableitung !
f(x)=ax2 +bx + c
f'(0) = 2ax + b = 0
2*a*0 + b = 0 --> b = 0
f(812) = 812 ² *a + c = 254
Nun kannst du mit dem Lösen der Gleichungssysteme die restlichen Variablen berechnen !
Zur Probe, c ist bei mir 65 !
Gruß Luis