Bestimmen Sie die Funktionsgleichung der ganzrationalen Funktion 3. Grades:
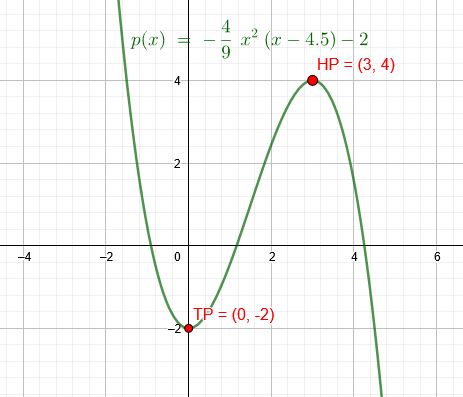
a) Tiefpunkt \(TP(0|-2)\) Hochpunkt \(HP(3|4)\)
Ich verschiebe den Graphen um 2 Einheiten nach oben:
Tiefpunkt \(TP´(0|0)\) Hochpunkt \(HP´(3|6)\)
\(f(x)=a*x^2*(x-N)\)
\(HP(3|6)\):
\(f(3)=a*3^2*(3-N)=9a*(3-N)\)→ \(9a*(3-N)=6\) → \(3a*(3-N)=2\)→ \(a=\frac{2}{9-3N}\)
\(HP(3|....)\):
\(f´(x)=\frac{2}{9-3N}*[2x*(x-N)+x^2]\)
\(f´(3)=\frac{2}{9-3N}*[2*3*(3-N)+3^2]=0\) → \(N=4,5\) \(a=\frac{2}{9-3*4,5}=-\frac{4}{9}\)
\(f(x)=-\frac{4}{9}*x^2*(x-4,5)\)
Nun um 2 Einheiten nach unten:
\(p(x)=-\frac{4}{9}*x^2*(x-4,5)-2\)
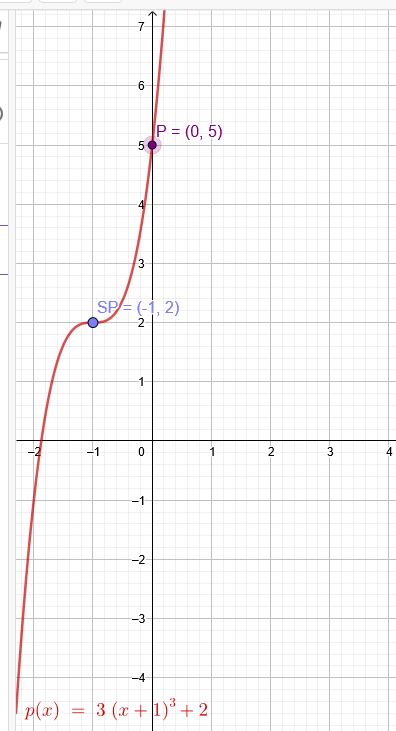
b) Sattelpunkt SP(-1|2) ; y-Achsenabschnitt=5 → \(P(0|5\)
Ich verschiebe den Graphen um 2 Einheiten nach unten:
\(SP´(-1|0)\) gibt eine dreifache Nullstelle:
\(f(x)=a*(x-(-1))^3=a*(x+1)^3\)
\(P´(0|3\)
\(f(0)=a*(0+1)^3=a=3\)
\(f(x)=3*(x+1)^3\)
Nun um 2 Einheiten nach oben:
\(p(x)=3*(x+1)^3+2\)