(a) bei einer eigentlichen Orthogonalmatrix müssen die Spaltenvektoren senkrecht aufeinander stehen und das System muss rechtsdrehend sein. Die Spaltenvektoren und ihr Skalarprodukt ist
$$\begin{pmatrix} \sqrt{3} \\ 1 \end{pmatrix} \cdot \begin{pmatrix} -1 \\ \sqrt{3} \end{pmatrix} = -\sqrt{3} + \sqrt{3}=0$$
Das Skalarprodukt st null (also orthogonal) und die Determinante ist >0 also 'eigentlich' - heißt nicht spiegelnd.
(b) Jede eigentliche Orthogonalmatrix mit normierten Spaltenvektoren kann man schreiben als
$$\begin{pmatrix} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{pmatrix}$$
hier ist \(\cos \phi = \frac{1}{2} \sqrt{3}\) und \( \sin \phi = \frac{1}{2}\) also ist \(\phi = \frac{\pi}{6} = 30°\)
(c) die Abbildung von \(u\) und \(v\) sind
$$ ^Au = Au+t= \frac{1}{2} \begin{pmatrix} \sqrt{3} & -1 \\ 1 & \sqrt{3}\end{pmatrix} \begin{pmatrix} \sqrt{3} \\ 1 \end{pmatrix} + \begin{pmatrix} 1 \\ 0 \end{pmatrix}= \begin{pmatrix} 2 \\ \sqrt{3} \end{pmatrix}$$
$$ ^Av = Av+t= \frac{1}{2} \begin{pmatrix} \sqrt{3} & -1 \\ 1 & \sqrt{3}\end{pmatrix} \begin{pmatrix}0 \\ 1 \end{pmatrix} + \begin{pmatrix} 1 \\ 0 \end{pmatrix}= \begin{pmatrix} \frac{1}{2} \\ \frac{1}{2} \sqrt{3} \end{pmatrix}$$
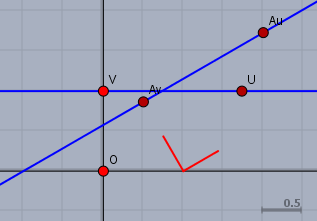
Die roten Balken zeigen die (halben!) Einheitsvektoren von \(\beta\) an
(d) hier ist nach dem Eigenvektor gefragt. Dazu schreibe ich die Abbildung \(\beta\) mit homogenen Koordinaten und bestimme von der Matrix den Eigenvektor
$$ \begin{pmatrix} \frac{1}{2}\sqrt{3} & -0,5 & 1\\ 0,5 & \frac{1}{2}\sqrt{3} & 0 \\ 0&0 &1 \end{pmatrix}$$
Die einzige reelle Lösung des charakterisctischen Polynoms ist \(\lambda=1\). Daraus folgt dann der Eigenvektor
$$ \approx \begin{pmatrix}0,5 \\ 1,866\\ 1 \end{pmatrix} \quad \Rightarrow w\approx \begin{pmatrix}0,5 \\ 1,866 \end{pmatrix}$$
letzteren habe ich nur nummerisch gerechnet