a und b derart bestimmen, dass sie Eigenvektoren von A sind

Question

es geht also wie gesagt um die Eigenvektoren von A.

In der Lösung wurde ´zunächst A*a = -2*(1,-3α,1)^T gerechnet. Ich verstehe das nicht ganz.. Wie kommt man zuerst darauf die Matrix mit dem Vektor zu multiplizieren, dann die -2 auszuklammern und schließlich dann schließen, dass für α=0 der Vektor a ein Eigenvektor zum Eigenwert -2 ist. 

Ich kenne die Eigenvektorberechnung nur über A-λE=0 , wobei λ ein Eigenwert des charakteristischen Polynoms ist. So bin ich auch hier auf die Lösung gekommen, aber die obige Methode scheint da effizienter zu sein wie erst Polynom aufstellen und LGS lösen.

Ich erkenne nicht den Zusammenhang zwischen dieser Berechnung mit der Herangehensweise aus der Lösung zu dieser Aufgabe hier (Matrix-Vektor Multiplikation, -2 ausklammern und dann α=0 setzen).

Vielleicht kann mir das jemand erklären warum man das so macht .

Answer 1

Guten Morgen Simon_W1997,

bei dieser Aufgabe musst Du keine Eigenwerte über das charakteristische Polynom berechnen. Du musst nur um die Bedeutung des Eigenvektors wissen. Wenn man den Eigenvektor einer Matrix A mit A multipliziert, dann erhält man λ (der Eigenwert) mal den Eigenvektor, mit dem Du die Matrix multipliziert hast. 

Wir führen also zuerst folgende Rechnung durch: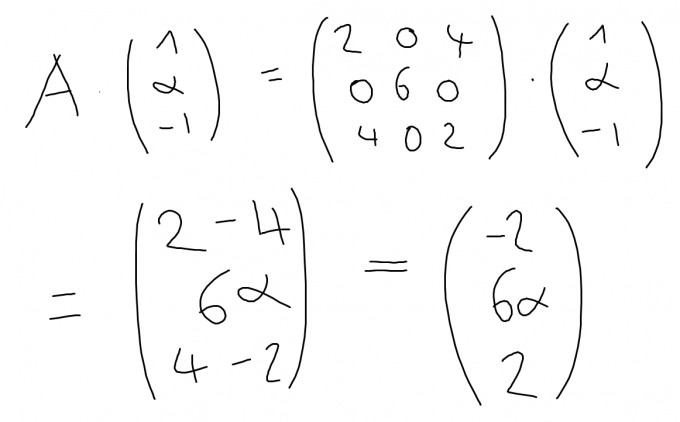

Wenn wir nun den so entstandenen Vektor mit dem ursprünglich als Eigenvektor angenommenen Vektor $$\left(\begin{matrix}1\\\alpha\\-1\end{matrix}\right)$$ vergleichen, dann sehen wir aufgrund des oberen und unteren Eintrags, dass wir diesen durch die Multiplikation mit -2 erhalten können.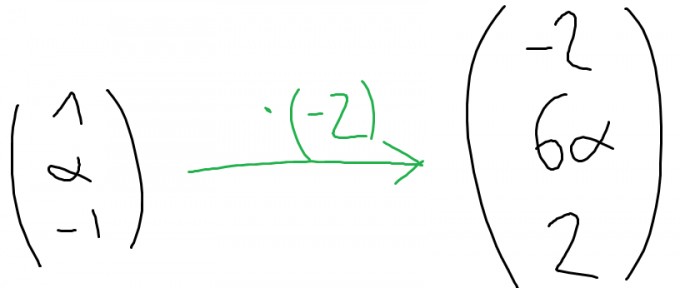

Nun sehen wir aber, dass $$-2\alpha \neq 6\alpha$$ Wenn Du allerdings $$\alpha=0$$ wählst, dann kannst Du den ursprünglichen Vektor durch die Multiplikation mit -2 vollständig in den Ergebnisvektor überführen, denn: $$\left(\begin{matrix}1\\0\\-1\end{matrix}\right)\cdot (-2) = \left(\begin{matrix}-2\\0\\2\end{matrix}\right)$$ Der Wert -2 ist übrigens der zum Eigenvektor 

$$\left(\begin{matrix}1\\0\\-1\end{matrix}\right)$$ passende Eigenwert λ.

Ich hoffe, dass ich Dir damit weiterhelfen konnte. Bei Rückfragen kannst Du Dich gerne wieder melden.

André, savest8

Comments

Hallo savest 8,sehr gut erklärt, :)