Kurvenschar, Wie hängt die Anzahl der Nullstellen vom Wert des Parameters a ab

Question

ich bräuchte Hilfe bei d) und f). d) weiß ich nicht, wie man sowas unterducht und f) verstehe ich einfach nicht.

Gegeben ist die Schar der in R definierten Funktionen fa: x-> -1/(3a^2)*x^3+5/4*x+2 mit a Element aus R+

Answer 1

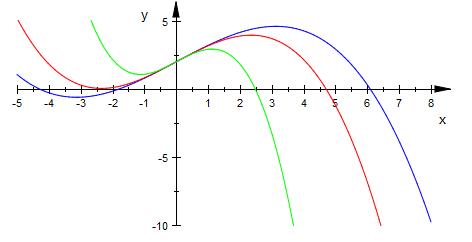
Es gibt einen Tiefpunkt und einen Hochpunkt.

Die x-Stelle des Tiefpunkts ist negativ
da a > 0

Die x-Stelle des Hochpunkts ist positiv
da a > 0

Der Graph geht also  von links kommend
zum Tiefpunkt, schneidet die y Achse bei y = 2
und geht dann zum Hochpunkt

Liegt der Funktionswert des Tiefpunkts ( oben
angegeben )
- oberhalb der x-Achse gibt es keine Nullstellen ( grün )
- auf der x -Achse dann 1 Nullstelle ( rot )
- unterhalb der x-Achse 2 Nullstellen ( blau )

Nach dem Hochpunkt geht es wieder
bergab zu einer weiteren Nullstelle.
Die Anzahl der oben angegebene Nullstellen
erhöht sich also noch um eine.

Comments

Vielen Dank goldusilberliebich! Könntest du Aufgabe f) auch graphisch darstellen? Ich verstehe nicht, wo die 2 Strecken mit der Länge 2 sich befinden und wie man dann die x-Koordinate ausrechnen kann

---

Sorry. Bitte Kommentar löschen. Ich kann nicht richtig lesen.

---

G_3,6 ( x ) = G_3,6 ( x + 2 )

Eine x-Stelle soll vom Funktionswert einer
( x -Stelle + 2 ) entsprechen.

x = -4.98 y = -1.05
x = 2.98 y = 5.05

Zu Fuß rechnen sollst du nicht.

Answer 2

Untersuche mal was passiert wenn der Tiefpunkt oberhalb, auf oder unterhalb der x-Achse liegt.

Eigentlich müsste man doch aber auch noch den HP mit Berücksichtigen.

Liegt der HP über der x.Achse und der TP unter der x-Achse gibt es 3 Nullstellen

Liegt der HP oder der TP auf der x-Achse gibt es zwei Nullstellen.

Liegt der HP unter der x-Achse oder der TP oberhalb der x-Achse gibt es nur eine Nullstelle.

Comments

Ach so, einfach nur eine was wäre wenn Aufgabe ohne Rechnung. Dann ist die ja doch nicht so schwer.  Könntest du mir noch bei f) helfen. Ich verstehe die Aufgabe einfach nicht. Zwei Strecken der Länge 2?? Ich würde einfach die Funktion gleichsetzen und den Schnittpunkt ausrechnen.. hm

---

Ich würde hier noch schreiben welche Werte  annehmen muss damit es 1, 2 oder 3 Nullstellen gibt.

und der Ansatz für f) ist

f(x) = f(x + 2)

Man bekommt dann

x = √3·(√(15·a^2 - 4) - 2·√3)/6 ∨ x = - √3·(√(15·a^2 - 4) + 2·√3)/6

Natürlich kann man bei Bedarf a vorher einsetzen. Aber es geht hier nicht darum es zu rechnen sondern nur zu beschreiben wie es geht.