Zeigen Sie, dass die Matrix C invertierbar ist genau dann, wenn Rg(C) = n ist.

Question

Es sei C ∈ Mn×n(K). Zeigen Sie, dass die Matrix C invertierbar ist genau dann, wenn Rg(C) = n ist. 

Ich habe leider nicht wirklich eine Idee, ich weiß was der Rang ist etc. aber ich weiß nicht wie ich die Definitionen bzw. Eigenschaften irgendwie verbinden soll, um das zu zeigen.

Schon mal danke für eure Hilfe :) 

Comments

Vom Duplikat:

Titel: Bitte Frage löschen, diese wurde shcon einmal gestellt

Stichworte: matrix,invertierbar,algebra,rang,quadratisch

Es sei C ∈  M_nxn(K). Zeigen Sie, dass die Matrix C invertierbar ist genau dann, wenn Rang(C) = n ist.

Answer 1

 

zu zeigen ist folgende Äquivalenz: $$C \text{ ist invertierbar }\Longleftrightarrow rg(C)=n$$ Der Beweis besteht aus zwei Teilen. 

Teil 1: $$C\text{ ist invertierbar } \Longrightarrow rg(C)=n$$ Wenn C invertierbar ist, dann ist die Standardabbildung f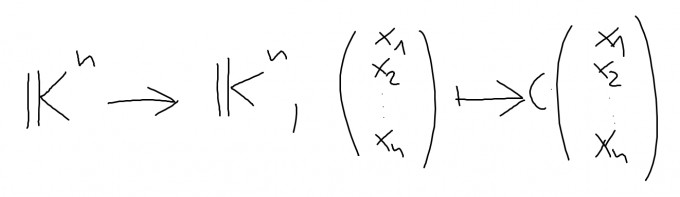

bijektiv. Daraus folgt, dass der Rang von C gleich n ist, denn das Bild von f  wird durch die Spalten von C erzeugt.

Teil 2: $$rg(C) = n \Longrightarrow C\text{ ist invertierbar}$$ Wenn der Rang gleich n ist, dann gibt es invertierbare Matrizen $$X,Y\in M_{n\times n}(\mathbb{K})$$ mit der Eigenschaft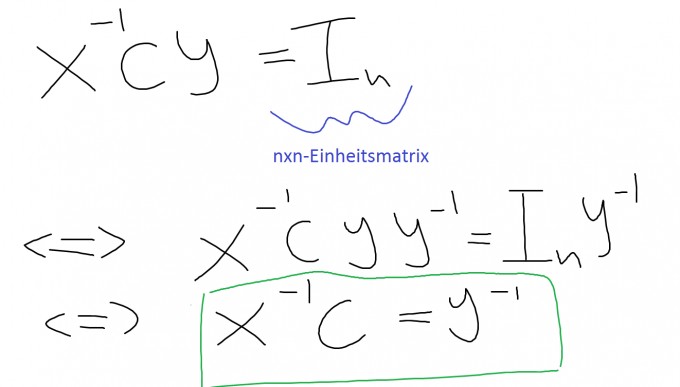 

Sei nun $$Z=Y\cdot X^{-1}$$ Dann folgt: $$ZC = Y\cdot \underbrace{X^{-1}\cdot C}_{=Y^{-1}\text{ siehe grüner Kasten}} = Y\cdot Y^{-1}=I_n$$ Demzufolge ist C invertierbar. 

q.e.d.

Die genutzten Annahmen solltet ihr in der Vorlesung besprochen haben. Falls nicht, kannst Du Dich gerne wieder melden.

André, savest8