f(x)=ax^2 und die Sinuskurve g(x)=b*sinx, 0<x<pi, schneiden ... Wie lauten die Funktionsgleichungen der kurven?

Question

Die Parabel f(x)=ax² und die Sinuskurve g(x)=b mal sinx, 0<x<pi, schneiden sich im Hochpunkt der Sinuskurve. Die von beiden Kurven umschlossene Fläche hat den Inhalt 6-pi.

wie lauten die funktionsgleichungen der kurven?

Comments

Die Parabel f(x)=ax^2 und die Sinuskurve g(x)=2 mal sinx, 0<x<pi, schneiden sich im Hochpunkt der Sinuskurve.

wie groß ist die von beiden kurven eingeschlossene fläche?

Answer 1

> schneiden sich im Hochpunkt der Sinuskurve

Hochpunkt der Sinuskurve ist (π/2 | b). Also ist f(π/2) = a·(π/2)² = b und somit a = 4b/π². Einsetzen liefert

        f(x) = 4b/π² x²

> Die von beiden Kurven umschlossene Fläche hat den Inhalt 6-pi.

Also ist ∫_0..π/2 (g(x) - f(x)) dx = ∫_0..π/2 (b·sin(x) - 4b/π² x²) dx = 6 - π. Bestimme das Integral; löse nach b.

Answer 2

f(x)=ax² und die Sinuskurve g(x)=b mal sinx,

Leider ist meine Antwort von gestern verschwunden

f ( x ) = a * x^2
g ( x ) = b * sin (x )

Schnittpunkt bei x = π / 2

f ( x ) = g ( x )
a * x^2 = b * sin (x )
a * (π / 2)^2 = b * sin (π / 2 )

b * 1 =  a * (π / 2)^2
b = 2.4674 * a

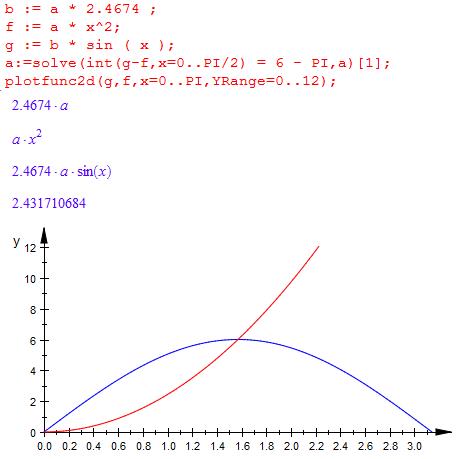a = 2.432
b = 6

Bei Bedarf nachfragen.