Question

Laplacescher Entwicklungssatz- Beweis

Brauche Hilfe bei diesem Beweis <3

Sei K ein Körper. Zeigen Sie:

\( \operatorname{det}\left(\begin{array}{cccc}{b} & {0} & {\cdots} & {0} \\ {a_{21}} & {a_{22}} & {\cdots} & {a_{2 n}} \\ {a_{31}} & {a_{32}} & {\cdots} & {a_{3 n}} \\ {\vdots} & {\vdots} & {} & {\vdots} \\ {a_{n 1}} & {a_{n 2}} & {\cdots} & {a_{n n}}\end{array}\right)=b \cdot \operatorname{det}\left(\begin{array}{ccc}{a_{22}} & {\cdots} & {a_{2 n}} \\ {a_{32}} & {\cdots} & {a_{3 n}} \\ {\vdots} & {} & {\vdots} \\ {a_{n 2}} & {\cdots} & {a_{n n}}\end{array}\right) \)

Comments

Oh ja bitte...brauche auch dringest Hilfe bei dem Beweis! Wäre super lieb, wenn einer mir helfen könnte.

---

Um was geht's eigentlich? Soll die gezeigte Formel ad hoc bewiesen oder bloss aus dem Entwicklungssatz hergeleitet werden?

---

Bewiesen und hergeleitet :-((

---

Man merkt, dass Du gar nicht verstanden hast, was ich gefragt habe.

---

In der Aufgabe steht beweisen:

Sei K ein Körper. Zeigen Sie:

---

Mit "Sie" bist Du gemeint. Wenn der Entwicklungssatz in der Vorlesung (die ich nicht hoere) schon dran war, dann ist der einfach auf den konkreten Fall anzuwenden (voellig trivial dann, Entwicklung nach der ersten Zeile). Ansonsten ist ein Ad-hoc-Beweis für die angegebene Formel verlangt. Was man dazu heranziehen kann, haengt wieder davon ab, was in der Vorlesung schon dran war.

---

der Satz kam in der Vorlesung noch nicht dran, deshalb ja meine Frage; Wie beweist man das Obenstehende?

---

Was schreibst Du dann "Laplacescher Entwicklungssatz" in den Betreff? Das ist doch einfach nur irrefuehrend. Deine Aufgabe ist es nicht, den Laplaceschen Entwicklungssatz zu beweisen. Beweisen sollst Du bloss gerade die angegebene Formel. Und was man dazu verwenden kann, musst Du wissen. Gib es an, ich hoere Deine Vorlesung nicht.

---

Ich komme echt nicht weiter... kannst du mir vielleicht mal ein paar konkretere Tipps geben?!

---

Haben noch nichts dazu in der Vorlesung gemacht

---

"Haben noch nichts dazu in der Vorlesung gemacht"

Naja ihr müsst ja wenigstens die Determinante einer Matrix definiert haben, ansonsten wäre die Aufgabe für euch ein Missverständnis und ihr müsst sie nicht lösen 

---

Im übrigen wäre es für das Stellen der Frage auch hilfreich, wenn der Hinweis unter der Aufgabe auch mit im Bild wäre

https://www.mathelounge.de/418067/fur-welche-x-%E2%88%88-%E2%84%9D-ist-die-matrix-a-1-2-1-1-x-1-2-0-x-invertierbar

---

Hier vielleicht der entscheidende HInweis:

https://www.mathelounge.de/418194/determinante-entwickeln-brauche--untenstehenden 

Answer 1

CarpeDiem,

bei der Lösung dieser Aufgabe kommt es besonders darauf an, was ihr bereits in der Vorlesung hattet und was nicht. Ich kann mir nicht vorstellen, dass ihr den Laplaceschen Entwicklungssatz zeigen sollt, weil das eigentlich Aufgabe für die Vorlesung ist (oder für ein Tutorium, wie es mal gehandhabt habe). Ich gehe davon aus, dass ihr den verwenden dürft, da sonst das Berechnen der Determinanten von Matrizen höherer Ordnung ziemlich schwierig wird. Wichtig bei diesem Satz ist die Formel, die gleichzeitig die (rekursive) Berechnungsvorschrift angibt: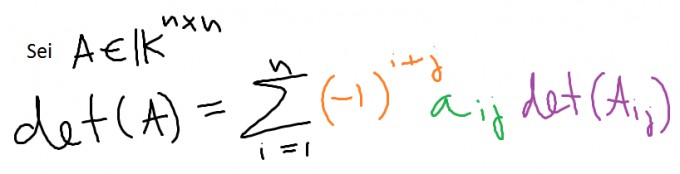 

Was steht da nun? i und j sind die Indizes zur Adressierung der Zeilen (i) und Spalten (j) in der Matrix. Orange gibt das Vorzeichen der Elemente in der Matrix an. Um das entsprechende Vorzeichen in der Matrix zu erhalten, addierst Du lediglich i und j. In einer 3x3-Matrix sähe das so aus: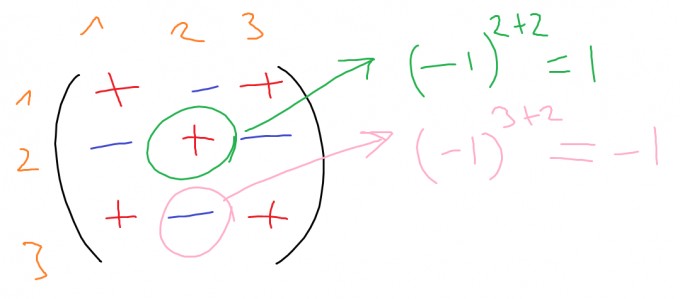 

Grün ist der Vorfaktor in der Zeile, nach der Du entwickelst. Das ist der Matrizeneintrag an der Stelle (i,j). Der violette Bestandteil ist die Determinante der "Streichmatrix". Was ist aber die Streichmatrix? Nun, das ist Matrix, die entsteht, wenn Du von dem Element $$a_{i,j}$$ ausgehend die i-te Zeile und j-te Spalte der Matrix streichst.

Beispiel:

 

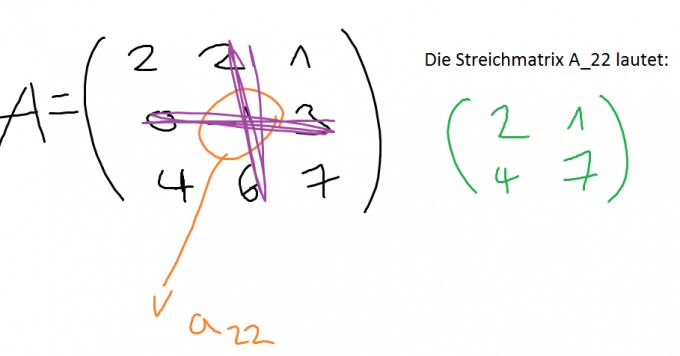
Du musst dieses Verfahren für jede Spalte (wenn Du nach einer Zeile entwickelst) oder für jede Spalte (wenn Du nach einer Zeile entwickelst) durchführen, also bis n. Zur Berechnung der Determinante der Streichmatrix verwendest Du dann wieder dieses Prinzip (Rekursion). Mit diesem Wissen ausgestattet ist die obige Aufgabe ziemlich leicht. Wenn Du die Determinante nämlich nach der ersten Zeile entwickelst, dann gilt: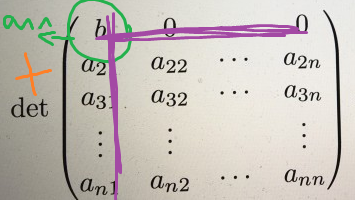 

Das Vorzeichen ist positiv, weil Du mit dem Element in der ersten Spalte und ersten Zeile beginnst, also $$(-1)^{1+1}=1$$ Der Vorfaktor ist b und die Streichmatrix ist der lila eingerahmte Matrizenausschnitt. Du erhältst dadurch die rechte Seite Deiner Gleichung. Warum bist Du an dieser Stelle bereits fertig? Ganz einfach: die Vorfaktoren im Rest der Zeile sind alle 0, d.h. selbst wenn Du für jedes Zeilenelement Vorzeichen, Streichmatrix etc. bestimmst, hat das auf das Ergebnis keinen Einfluss.

Konnte ich Dir weiterhelfen?

Weiterhin viel Erfolg im Studium und beste Grüße!

André, savest8

Comments

Oben sagen die Herrschaften auf Nachfrage, dass der Entwicklungssatz nocht nicht besprochen wurde. Aber vielleicht wissen sie das ja selber nicht. Kann auch sein.

---

Hallo Fakename,

sorry, die Kommentare habe ich mir nicht durchgelesen bzw. zu spät gesehen, da der Wunsch zur Bearbeitung durch mich an anderer Stelle erfolgte.

Wenn dem so ist, dann kann der Fragesteller meine Antwort gerne als Lernhilfe nutzen;-)

André, savest8

---

Vielen Dank für deine Antwort, soweit habe ich das verstanden. Doch wie würde man das jetzt formal beweisen?

---

Ich verlinke an dieser Stelle noch einmal ein kurzes Lernvideo, in dem der Laplacesche Entwicklungssatz veranschaulicht wird. Das ist für zukünftige Leser dieser Antwort gedacht: https://youtu.be/ASdGE6N3rOw?t=27s

Answer 2

Setze \(a_{11}=b\) und \(a_{12}=\ldots=a_{1n}=0\).  Dann: $$\begin{aligned}\det(a_{ij})&=\sum_{\pi}\varepsilon(\pi)\,a_{1,\pi(1)}a_{2,\pi(2)}\ldots a_{n,\pi(n)}\\ &= b\!\!\sum_{\pi(1)=1}\!\!\varepsilon(\pi)\,a_{2,\pi(2)}\ldots a_{n,\pi(n)}\\ &= b\cdot\det(a_{ij})_{i,j=2}^n\end{aligned}$$