Absolute Minimal- und Maximalstellen bestimmen.

Question

Bestimmen Sie für f₁(x) := x^3 exp (-(x^2/6) und für f₂(x) := -(x/2) + sin(x) jeweils die absoluten Minimal- und Maximalstellen auf ]2,∞[ und [0,∞[ (sofern solche überhaupt existieren).

Comments

Bestimmen Sie für f₁(x) := x^3 exp (-(x^2/6)) und für f₂(x) := -(x/2) + sin(x)  : ℝ → ℝ jeweils alle kritischen Punkte und deren Typ ( Minimal-/ Maximalstelle oder Sattelpunkt).

---

Bilde die ersten 3 Ableitungen.

Wie man Minimal-/ Maximalstelle oder Sattelpunkt berechnet, solltest du wissen.
Falls nicht, schau bei wiki nach.

---

Mein Problem ist das Bilden der ersten drei Ableitungen...

---

f 1: Produkt- und Kettenregel anwenden.

f 2. summandenweise ableiten

---

Könntest du mit vielleicht zeigen, wie das genau in den Fällen geht? :/

---

u= x^3 --> u '=3x^2

v= e^{-x^2/6} --> v '= e^{-x^2/6}* (-2/6*x)

Bastle das zusammen. Probuktregel sollte bekannt sein.

---

u*v' + u'*v?

---

Jawoll! :)

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

---

Und wie geht das mit der Ableitung bei f₂?

---

summandenweise ableiten. Das ist ist sehr einfach.

Tipp:

-(x/2) = -1/2 *x

---

Und das wäre abgeleitet dann einfach -1/2 oder?

Answer 1

Hallo Chica,

1) ich schreibe f₁(x) = f(x)

f: [ 2 , ∞ [  → ℝ  ,  f(x) = x³ * exp( - x²/6 )   

mit der Produktregel erhältst du  

f '(x) = 1/3 · x²  ·exp( - x²/6) ·(9 - x²)  = 1/3 · x²  ·exp( - x²/6)  · (3 - x) · (3 + x)

f ' hat bei x=3 eine Nullstelle mit Vorzeichenwechsel von + nach -  →  Maximalstelle  

  x= -3 ∉ D_f

x=0  ist eine doppelte Nullstelle → Sattelpunkt   

lim_x→∞ f(x) = 0 , weil der e-Term ( → 0) überwiegt

f(2) = 8·e^-2/3 ≈ 4.107  

f(3) = 27·e^-3/2 ≈ 6,025

in D = [ 2 , ∞ [  gibt es also nur die absolute  Maximalstelle  x = 3      (#)

#

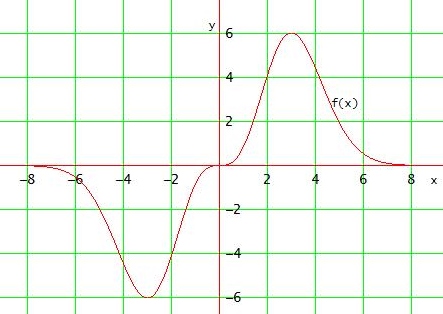
Sollte der 1. Funktionsterm auch noch mit  D = [ 0 , ∞ [ betrachtet werden, dann hätte man noch die absolute Minimumstelle x = 0

----------

2)  ich schreibe f₂(x) = f(x)  

D_f = [ 0 , ∞ [

f(x) = - x/2 + sin(x)  →  f '(x) = -1/2 + cos(x)  

f '(x) = 0   ⇔_D  cos(x) = 1/2  ⇔  x = π/3 + k * 2π  oder x = 5π/3 + k * 2π   [ mit k∈ℕ ]  

f(π/3) = √3/2 - π/6 ≈ 0,34 , die Funktionswert bei den anderen Nullstellen von f ' sind  [wegen sin(x)≤1]  negativ.

f(0) = 0  und  lim_x→∞ f(x) = - ∞  →  es gibt nur die absolute Maximalstelle x = π/3  

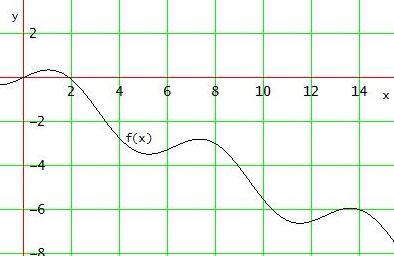
Gruß Wolfgang

Comments

x=0  ist eine doppelte Nullstelle → Sattelpunkt

x=0  ist eine dreifache Nullstelle → Sattelpunkt

Bei doppelter  Nullstelle wäre es ein Extremwert

Answer 2

Zur Kontrolle: f₁(x)=x³·e^-x2/6 f₁'(x)=(x²·e^-x2/6_·(9-x²))/3 Nullstellen der ersten Ableitung x=±3, x=0.

f₁''(x)=(x·e^-x2/6·(x⁴-21x²+54))/9 Nullstellen der zweiten Ableitung x=±3√2, x=±√3, x=0

Sattelpunkt bei x=0. Weitere Wendepunkte bei x=±3√2, x=±√3. (Wendepunkte noch mit der dritten Ableitung bestätigen). Hochpunkt bei x=3, Tiefpunkt bei x=-3.