Gebrochenrationale Funktion - Kühlturm - Betonmenge berechnen

Question

Die innere Querschnittslinie eines 200 m hohen Kühlturms kann mit der Funktion f(x)= $$ \frac { 1 }{ 0,025x-0,075 } -10 $$ beschrieben werden.
(1 Längeneinheit = 10m)

So eine Frage der Aufgabe lautet, welche Betonmenge verbaut wurde(Hautdicke 22 cm)?

Leider kann ich nicht viel mit der Funktion anfangen, da ich nicht weiß, was sie genau bedeutet. Sie hat ja bei x = 3 eine Definitionslücke die mich ein wenig Verzweifeln lässt.
Ist als Querschnittslinie der Durchmesser gemeint?

Ich dachte das das Integral der Funktion von 0 bis 20 die Summe aller Durchmesser ist. Wenn man das addiert mit 22 cm und dann die Höhe noch dazunimmt, hat man doch das Volumen des Betons? Oder liege ich da Falsch ?

Ich hoffe einer kann mir Helfen. Danke :)

Comments

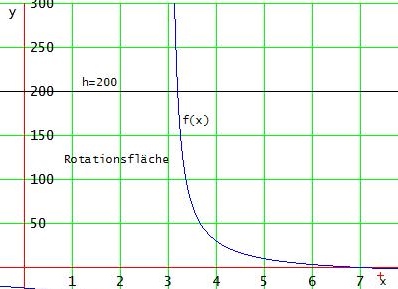
Ich denke, die dargestellte Rotationsfläche, die im 1.Quadranten von f(x) berandet wird, soll um die y-Achse rotieren. 

V_y  =  π · ₀∫²⁰⁰  f^-1(y)  dy    mit  der Umkehrfunktion  f^-1(y) = 40 / (y + 10) + 3  von f(x).

Außerdem müsste dann die Funktion g(x), deren Punkte um 0,22 senkrecht zu G_f (also ständig in eine andere Richtung) verschoben sind, um die y-Achse rotieren, denn nur dann wäre die Betonhaut überall 22 cm dick.

 Dann könnte man die Differenz beider Volumina ausrechnen.

Zur Berechnung von g(x) fällt mir aber leider nichts Vernünftiges ein.

Vielleicht ist aber die Aufgabenstellung bzgl. der Betonhaut auch völlig unklar formuliert.

Umkehrfunktion f^-1:

f(x) = y =  1/(0.025·x - 0.075) - 10 

y + 10  = 1 / (0.025·x - 0.075)

0.025·x - 0.075 = 1 / (y + 10)

0.025·x  =  1 / (y + 10) + 0,075

   x  =  40 / (y + 10) + 3

Rotationsvolumen bzgl. f(x): 

V_y  =  π · ₀∫²⁰⁰  f^-1(y)  dy   = π · ₀∫²⁰⁰ ( 40 / (y + 10) + 3 ) dy  = [ 40 · ln(y+10) + 3y ]₀²⁰⁰

        =  40 · ln(210) + 600 - 40 · ln(10)  ≈ 721,780   [m³]

Answer 1

Ich würde es wie folgt rechnen wenn die Betondicke in horizontaler Richtung gemessen wird. Für andere Messverfahren dürfte es aber eher hoffnungslos sein, dass schnell lösen zu können.

y = 1/(0.025·x - 0.075) - 10

Umkehrfunktion bilden

y = 40/(x + 10) + 3

Rotationsintegral

V = ∫ (x = 0 bis 20) (pi·((40/(x + 10) + 3 + 0.022)^2 - (40/(x + 10) + 3)^2)) = 14.399 VE = 14399 m³

Comments

PS: Den Kühlturm stelle ich mir von der Seite wie folgt vor

---

Danke,das mit dem Rotationsintegral ist mir nicht eingefallen.

Aber der Kühlturm ist abgebildet, wie ein klassischer Turm vom AKW der oben wieder etwas breiter als im Rumpf ist. Deshalb ist deine Abbildung irgendwie nicht ganz korrekt, wenn ich mich nicht täusche. Aber diese Berechnung sollte reichen ;)

Answer 2

ich habe zunächst die Umkehrfunktion gebildet damit
der Kühlturm ( schornsteinförmig ) um die x-Achse
rotieren kann.

Blaue Kurve
f ( x ) = 40 / (x + 10) + 3

Betondicke 0.22 m
Rote Kurve = blaue Kurve nach oben verschoben
f ( x ) = 40 / (x + 10) + 3 + 0.22

Jetzt das Rotationsvolumen von Rot bestimmen
und das Rotationsvolumen von Blau abziehen.

Im Fußbereich dürfte es nicht ganz stimmen.
Hier könnte man auch noch zusätzlich um 0.22 m nach
rechts verschieben.

f ( x ) = 40 / ( ( x - 0.22 ) + 10) + 3 + 0.22

So viel zunächst

Nachfrage : ist der Kühlturm 200 m oder 20 m hoch ?
Beides ist oben angeführt.

Comments

Der Turm ist 200 m hoch (20 wegen der Längeneinheit).

Aber  warum verschiebt man den Turm am Fuß nach rechts?

---

Umkehrfunktion
f ( x ) = 40 / ( x + 10) + 3

Radius
r = f ( x )
Fläche
A = r^2 * π
Stammfunktion
S ( x ) = ∫ A dx
Volumen
V = [ S ( x ) ] zwischen 0 bis 20

Volumen im m^3
V * 10^3

Die erste obere blaue Zeile gilt nicht.


Die blaue Kurve zeigt die Innenlinie des Kühlturms.
Dann addiert sich 0.022 Betonstärke hinzu.

Der Mathecoach ist mit der Betonstärke nach innen gegangen
3 - 0.022 und hat daher etwas weniger heraus.

Zu : mit nach rechts verschieben male ich noch ein Bildchen.

mfg

---

Die erste Skizze zeigt die Innenlinie und eine
um 0.022 m nach oben verschobene Kurve.


Ganz richtig wäre aber :
die Betonstärke steht immer als Normale
mit 0.022 auf der Innenlinie.
Vermute ich einmal.
Dann müßte man überlegen welche Funktion
es sich für die Außenlinie ergibt.

---

Ah ok so ist das also, danke für deine Hilfe!!!

---

Halt: Eine Frage hätte ich dann doch noch: Was genau sagt mir die gegebene Funktion der Querschinttslinie f(x)=1/(0.025·x - 0.075) - 10 aus?

--> Wenn ich für beispielsweise x=20 setze, kommt dann der Durchmesser des Turmes in 200 m Höhe raus? Oder wie ist das zu Verstehen?

Danke

---

x = 20
f ( x ) ist der Funktionswert an der Stelle x und
entspricht dem Radius des Rotationskörpers.
Durchmesser wäre mal f ( x )  * 2