Kern / Basis des Kerns einer Matrix bei vollen Rang

Question

hallo allerseits,

angenommen eine Matrix hat vollen Rang. heißt das dann, dass Kerns(M)=0 und Basis_(ker(M)) = {}  ?

Answer 1

das ist in der Tat richtig. Eine Idee dafür kannst Du z.B. durch den Rangsatz bekommen: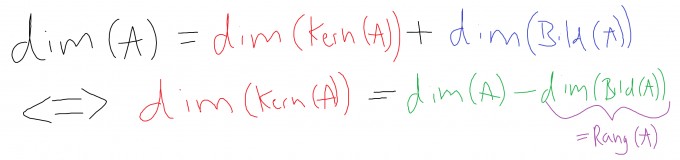 

Die Matrix A (bzw. M) hat vollen Rang. Es sei $$\dim{(A)}=n\in\mathbb{N}$$ Unter den gegebenen Voraussetzungen gilt: $$rg(A)=n $$ und mit dem Rangsatz folgt: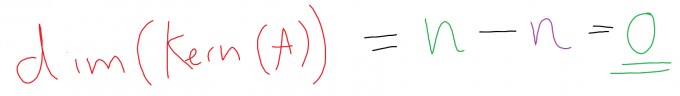 

Ersetzen wir nun A durch die von Dir gewählte Bezeichnung M, so können wir den Kern durch $$Kern(A)=\{0\}$$ wobei die 0 der Nullvektor ist (Nullvektorraum), angeben. Dieser hat als Basis die leere Menge, also: 

Achte aber darauf, dass Du Begriffe Basis und Dimension nicht vermischst/verwechselst. Ein gutes Video, das ich an dieser Stelle mit der Community teilen möchte, gibt es von Daniel Jung: 

Ich hoffe, dass ich Dir damit weiterhelfen konnte! Melde Dich bei Rückfragen gerne wieder!

André, savest8

Answer 2

Ja. Das sollte so stimmen.

Vgl. hier: https://de.wikipedia.org/wiki/Nullvektorraum

Kern(M)={0} (diese 0 ist der Nullvektor)

und Basis_(ker(M)) = {}  ?

Comments

Hallo Lu,

das ist richtig. Ich habe dem Fragegesteller noch einen Erklärungsansatz über die Dimensionsformel/den Rangsatz gegeben. Dadurch bekommt man noch eher ein Gespür für die Zusammenhänge.

PS: Ich schätze Deine Beiträge sehr;-) Weiter so!