In der Zahlenebene sieht das doch so aus:
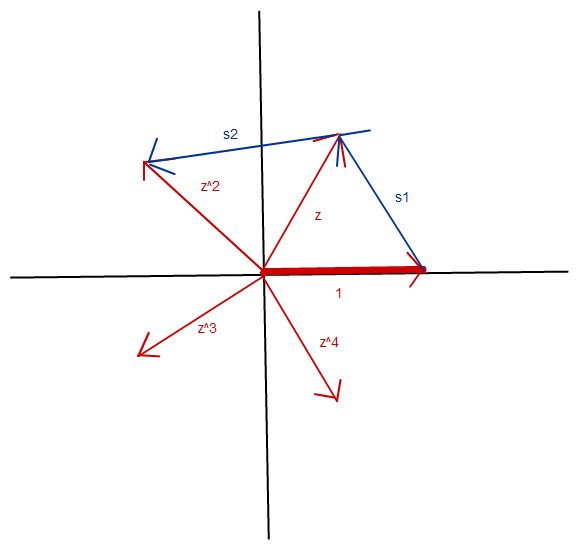
wegen z
5 =1 gilt auch |z|
5 = 1 also haben alle Potenzen von z den Betrag 1.
Damit wirkt die Multiplikation einer komplexen Zahl mit z wie eine Drehung um den
Winkel arg(z). Der ist hier 360° / 5 = 72° .
Also sind die Dreiecke, die immer aus z
k und z
k+1 gebildet werden alle gleichschenklig
mit dem Winkel von 72° an der Spitze und damit kongruent, also alle Basen (die blauen)
gleich lang. Und es gilt für eine halbe Basislänge s/2 = sin(36°) also s = 2*sin(36°).
Und die Diagonalen sind ja immer die Verbindungslinien von zwei nicht benachbarten
Ecken, also Basen im gleichschenkligen Dreieck mit Schenkellänge 1
und an der Spitze einem Winkel von 2*72° = 144° .
Für eine halbe Diagonale gilt also d/2 = sin(72°) also d=2*sin(72°).