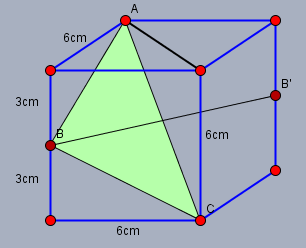
wenn der Würfel ein Volumen von \(216\text{cm}^2\) hat, so ist seine Kantenlänge \(6\text{cm}\). Die Strecke \(AB\) lässt sich dann nach Pythagoras berechnen:
$$AB=\sqrt{(6\text{cm})^2+(3\text{cm})^2}=3\sqrt{5}\text{cm} \approx 6,708\text{cm} $$
Die Strecke \(BC\) ist genau so lang wie \(AB\) und für die Berechnung der Strecke \(AC\) bestimmt man zunächst die Diagonale \(d\) (schwarz eingezeichnet) - \(d=\sqrt{(6\text{cm})^2+(6\text{cm})^2}=6\sqrt{2}\text{cm}\). Die Strecke \(AC\) läuft wieder über den Pythagoras, da \(d\) auf der senkrechten Kante, die von \(C\) ausgeht, senkrecht steht.
$$AC=\sqrt{ (6\text{cm})^2 + (6\sqrt{2}\text{cm})^2 }=6\sqrt{3}\text{cm}$$ Der Umfang \(U\) ist dann
$$U=AB+BC+AC=2\cdot 3\sqrt{5}\text{cm}+ 6\sqrt{3}\text{cm} \approx 23,81\text{cm}$$
Die Höhe des Dreiecks ist identisch zur Hälfte der Strecke \(BB\prime\), die wiederum ist so lang wie \(d\) (s.o.) Daraus folgt dann die Fläche
$$F=\frac{1}{2}AC \cdot \left( \frac{1}{2} BB\prime\right)=\frac{1}{2}6\sqrt{3}\text{cm} \cdot \frac{1}{2}6\sqrt{2}\text{cm}=9\sqrt{6}{\text{cm}}^2 \approx 22,05 {\text{cm}}^2$$