Sei K (x,y,z)=(x,y,z) das Vektorfeld ...... Berechnen Sie den Fluss von K durch F mit und ohne den Satz von Gauß !

Question

Ich komme mittels dem Satz von Gaus über das dreifach Integral der Divergenz von K auf ein Ergebnis von 48 PI.

Bei der Lösung ohne Satz von Gauß bin ich mir nicht ganz sicher wie ich hier vorgehen soll. Ich denke damit ist doch eine Vorgehensweise über das Oberflächenintegral gemeint ?!?!
Nunja hab mir versucht das Oberflächenintegral zusammenzustückeln und bin irgendwie auf kein Ergebnis gekommen, das mit 48PI übereinstimmt.
Vielleicht könnte mir jemand bei der Lösung dieser Aufgabe helfe.
Lg

Answer 1

zerlege den Viertelzylinder in 5 Teilflächen und berechne dann jeweils den Fluss:

1) Deckfläche

2) Grundfläche

3) Mantel 

4) ,5) die inneren Begrenzungsebenen

Deck- und Grundfläche:

$$ { F }_{ 1 }=\int\vec{ K }d\vec{ A }=\int_{0}^{\pi/2}d\phi\int_{0}^{4}rdr\begin{pmatrix} rcos(\phi)\\rsin(\phi)\\5 \end{pmatrix}\begin{pmatrix} 0\\0\\1 \end{pmatrix}\\=\frac { 5\pi }{ 4 }*16=20\pi\\{ F }_{ 2 }=\int\vec{ K }d\vec{ A }=\int_{0}^{\pi/2}d\phi\int_{0}^{4}rdr\begin{pmatrix} rcos(\phi)\\rsin(\phi)\\0 \end{pmatrix}\begin{pmatrix} 0\\0\\1 \end{pmatrix}=0 $$

Mantel:

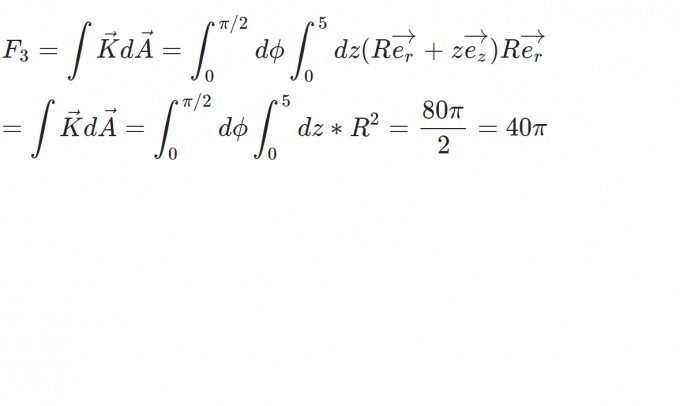
 -x=0 Ebene (mit kartesischen Koordinaten):

$$ { F }_{ 4 }=\int\vec{ K }d\vec{ A }=\int\begin{pmatrix} 0\\y\\z \end{pmatrix}\begin{pmatrix} 1\\0\\0 \end{pmatrix}=0$$

Dasselbe für y=0

Also Gesamtfluss=60π

Wenn man da Volumenintegral berechnet, erhält man:

$$ F=\int div\vec{ K }dV=\int_{0}^{\pi/2}d\phi\int_{0}^{5}dz\int_{0}^{4}rdr*3=60\pi $$

Das unterscheidet sich von der Oberfläche eines Viertelzylinders (48π), weil er nicht symmetrisch zum Ursprung liegt.