ich bin kürzlich auf eine komplizierte Rechenaufgabe gestoßen, die ich nicht zu lösen vermag, und hätte gehofft hier etwas Hilfe zu bekommen.
Und zwar sollen Fahnenmasten auf 3 Gebäude mit Seilen miteinander verknüpft werden und die Frage ist wieviele Meter Seil für dieses Unterfangen benötigt würden. Ich habe hierfür die folgende Skizze gegeben
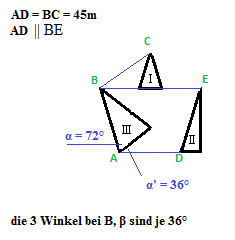
in der Skizze stellen 2 gleichschenklige (Dreieck I und III) und ein rechtwinkliges Dreieck (Dreieck II) die 3 Gebäude dar, auf denen sich die Fahnenmasten befinden. Auf jedem Gebäude befindet sich jeweils ein Fahnenmasten und zwar genau auf dem Inkreismittelpunkt des jeweiligen Dreiecks.
Um zu wissen wie viel Meter Seil benötigt wird, müsste ich also den Umfang des Dreiecks berechnen, das sich ergibt wenn ich die 3 Inkreismittelpunkte der Dreiecke verbinde.
Leider hab ich es mit den vorhandenen Angaben noch nicht einmal geschafft die Seitenlänge eines der Dreiecke zu berechnen. wie sich dann die Distanz zwischen den einzelnen Inkreismittelpunkten berechnen lässt bin ich auch noch völlig im Dunkeln. Ich hoffe nun, dass ich hier etwas Hilfe bekommen kann.
und bedanke mich im voraus für jede Unterstützung.