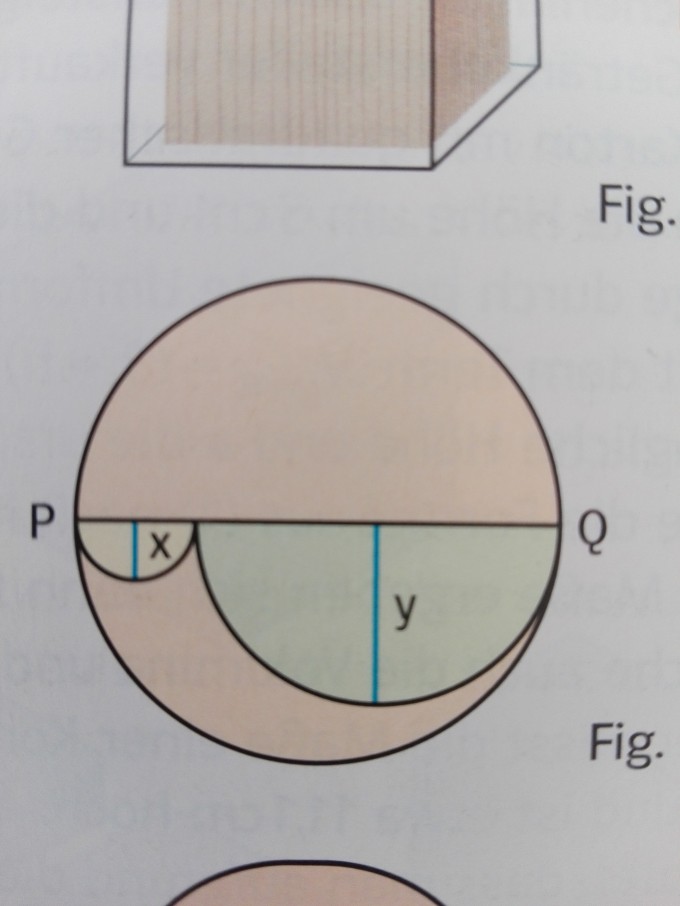
a)Zeige, dass der Weg von P nach Q entlang des großen Halbkreises genauso lang ist wie der Weg entlang der beiden kleinen Halbkreise. Stelle hierzu geeignete Terme auf und vergleiche sie.
b) Zeige,dass die Weglänge immer noch gleichlang ist,wenn drei Halbkreise von P nach Q führen.
Ich sitze schon länger an dieser Aufgabe, habe auch Ansätze doch komme irgendwie nicht weiter... Danke schon Mal für die Lösungen;))