Eine Leiter ist genauso lang wie ein Mauer hoch ist

Question

Aufgabe: Eine Leiter ist genauso lang wie eine Mauer hoch ist. Lehnt man die Leiter 20 Zentimeter unter dem oberen Mauerrand an so ist sie unten 1, 2 m von der Mauer entfernt. Wie lange ist die Leiter?

Answer 1

Die Höhe der Mauer sei $m$. Dann gilt laut Satz des Pythagoras

        $(m-0{,}2)^2 + 1{,}2^2 = m^2$.

Löse diese Gleichung.

Answer 2

Hallo Sarah,

mache Dir eine Zeichnung

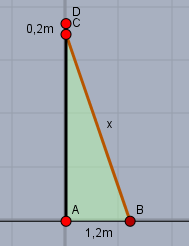
Die Wand soll die Strecke $|AD|$ sein. Die Leiter ist die Strecke $|BC|$ und hat die gleiche Länge $x$ wie die Wand hoch ist. Kannst Du den Pythagoras für das markierte Dreieck $\triangle ABC$ aufstellen?

$$\begin{aligned} (x-0,2)^2 + 1,2 ^2 &= x^2 \\ x^2 - 0,4x + 0,04 + 1,44 &= x^2 \\ 1,48 &= 0,4 x \\ x &= 3,7\end{aligned}$$

Answer 3

hallo,

x: Mauerhöhe , Leiterlänge         Pythagoras anwenden     1,2m =120cm

x² =(x-20)² +120²

x² = x² -40x +200+14400  | sortieren

40x = 14600                    | : 40

     x= 370cm

Die Leiter ist 370cm oder 3,7 m lang.

Answer 4

(h-0,2)²+1,2²=h². Dann ist h=3.7 m.