hier ist eine ausführliche Skizzierung des Rechenwegs (den Fall \(X=0\) kannst Du ignonieren):
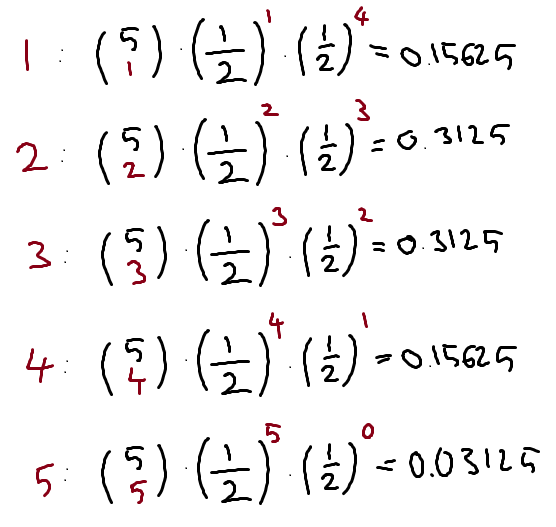
Nun berechnest Du:
$$E(X)=1\cdot 0.15625 + 2\cdot 0.3125 + 3\cdot 0.3125 + 4\cdot 0.15625 + 5\cdot 0.03125=2.5$$
Mit \(1.78\) hast Du Dich leider verrechnet.
Noch einfacher hättest Du die Aufgabe mit der Formel $$E(X)=n\cdot p$$ lösen können, wobei \(p=\dfrac{1}{2}\) und \(n=5\). Es ergibt sich ebenfalls: $$E(X)=\dfrac{1}{2}\cdot 5=2.5$$
André, savest8