Quadratische Ergänzung. Warum ist das so?

Question

Ich stehe hier vor einem Problem. Ich habe zur Übung die quadratische Ergänzung gemacht.

f(x) = x² +6x

f(x) = (x²+6x+9) -9

f(x) = (x+3)²-9

Allerdings wird in der Lösung kein -9 angezeigt. Bedeutet es, dass es falsch wäre mit der -9?

und warum ?

Hoffe jemand kann mir helfen.

LG

Answer 1

Quadratische Ergänzung kannst du geometrisch folgendermassen anschauen:

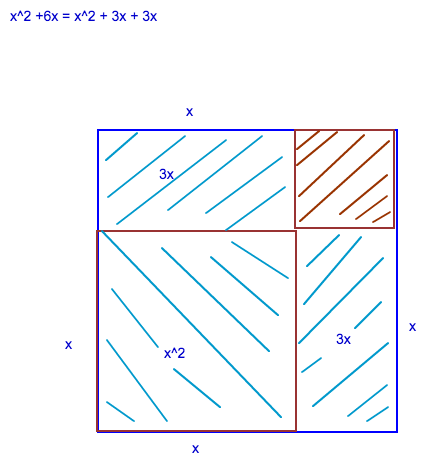
Du sollst die 3 blauen Felder so ergänzen, dass ein Quadrat entsteht.

Ergänzung ist nun das rote Quadrat oben. Also 3*3 = 9

Nun kannst du der Abbildung entnehmen:

Grosses Quadrat = Summe von 4 Teilen

(x+3)^3 = x^2 + 3x + 3x + 9 = x^2 + 6x + 9 

Zum gegebenen blauen Teil ist die rote 9 ergänzt worden. (quadratische Ergänzung: Ergänzung zu (x+3)^2)

Das ist selbstverständlich nicht dasselbe wie x^2 + 6x und darf in Äquivalenzumformungen nicht ohne Kompensationen gemacht werden.

Wie in den vorhandenen Antworten erwähnt, ist die konkrete Fragestellung wichtig. Du hast dein f schon korrekt umgeformt. 

Answer 2

deine Lösung ist genau richtig  :-)

Gruß Wolfgang

Answer 3

f(x) = x² +6x

f(x) = (x²+6x+9) -9

f(x) = (x+3)²-9

hast du richtig umgeformt.

Die quadratische Ergänzung ist die 9, die man addiert (erfindet), damit sich in der nächsten Zeile eine Klammer im Quadrat ergibt. Die -9 ist als Kompensation nötig, wenn links immer noch f(x) steht. 

Wie ist die Fragestellung ganz genau?

Man kann die quadratische Ergänzung verschieden einsetzen: Z.B. bei Gleichungen:

x^2 + 6x = 0           | + 3^2

x^2 + 6x + 9 = 9

(x+3)^2 = 9

(x+3) = ±3 

x = 3±3

x_(1) = 6, x_(2) = 0. 

Answer 4

Wenn nur nach der quadratischen Ergänzung gefragt ist, so ist 9 richtig (Quadrat der halben Vorzahl von x). Wenn aber die Umformung der Gleichung in eine gleichbedeutende verlangt wird, ist rechts 9-9=0 zu addieren.