Die Punkte A, B,C und D bilden ein Parallelogramm. Bestimmen Sie den Punkt D

Question

Hallo liebe Mathelounge,

leider eine weitere Frage zur Klausurvorbereitung.

Gegeben Sind 3 Punkte A = (-1 2 3), B = (0 5 4) und C = (3 1 0). Diese bilden mit dem gesuchten Punkt D ein Parallelogramm.

 


Nun soll ich D bestimmen. Da ich weiß, das für die Vektoren BD und AC gilt:  BD||AC, habe ich erst den Vektor AC bestimmt und diesen dann "nach rechts verschoben" in dem ich ihn zum Punkt B hinzuaddiert habe.

In den Lösungen ist vorgegeben, dass das nun auch schon der gesuchte Punkt D wäre - und hier ist mein Problem.
Der Punkt D wird ja eigentlich als Ortsvektor vom Ursprung dargestellt - in diesem Fall wäre er laut Lösung aber der Vektor zwischen B und D?

Müsste ich nicht eigentlich erst noch OD (also den eigentlich Ortsvektor zum Punkt D) bestimmen, in dem ich rechne:

BD = OD - OB    |+ OB
BD + OB = OD

Das Ergebnis wäre dann ja D = (4 9 5)


Ich bin wie immer für jede Hilfe dankbar :)

Answer 1

Bevor Du nach dem Punkt \(D\) suchst, solltest Du Dir darüber im Klaren sein, ob das Parallelogramm ABCD oder ABDC das gesuchte ist. Ist das nicht definiert, so gibt es zwei Lösungen wie folgende Skizze zeigt

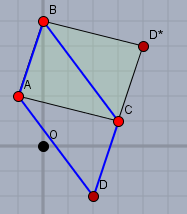
Der Vektor \(\vec{AB}\) ist

$$\vec{AB}=\vec{OB} - \vec{OA}=\begin{pmatrix} 0+1 \\ 5-2 \\ 4-3\end{pmatrix}=\begin{pmatrix} 1 \\ 3 \\ 1\end{pmatrix}$$

Je nachdem, ob Du ihn zu \(\vec{OC}\) addierst oder subtrahierst bekommst Du die eine oder andere Lösung

$$\vec{OD}=\vec{OC} - \vec{AB}=\begin{pmatrix} 3-1 \\ 1-3 \\ 0-1\end{pmatrix}=\begin{pmatrix} 2 \\ -2 \\ -1\end{pmatrix}$$ ist auch die von Roland für das Parallegramm ABCD - oder

$$\vec{OD}=\vec{OC} + \vec{AB}=\begin{pmatrix} 3+1 \\ 1+3 \\ 0+1\end{pmatrix}=\begin{pmatrix} 4 \\ 4 \\ 1\end{pmatrix}$$ die nach Deiner Zeichnung oben für das Parallelogramm ABD*C.

Und ja - zu Deiner Frage: Der Punkt \(D\) ist der Ortsvektor von \(O\) nach \(D\). Aber wie Du auf (4,9,5) kommst ist mir schleierhaft? nach Deiner Rechnung müsste dort (4,4,1) - also \(D^*\) heraus kommen.

Comments

Es gibt immer drei Lösungen...

---

stimmt - aber das \(A\) gegenüber zu \(B\) liegt, steht hier nicht zur Debatte

---

Was soll das heißen, "A gegenüber zu B"?

---

Sollte heißen: Der Punkt \(A\) liegt im Parallelogramm dem Punkt \(B\) gegenüber. Das wäre die dritte Möglichkeit wie folgende Skizze zeigt

Das ergäbe das Parallelogramm ACBD** mit den blauen Seiten. Das Parallelogramm ABCD ist das wie es in der Schule gelehrt wird (s. Lus und Rolands Antworten) und ACD*B entspricht dem in der Aufgabestellung gezeichnetem.

Gruß Werner

Answer 2

AB=(1;3;1) OC - AB = OD also (3;1;0) - (1;3;1)=(2;-2:-1) Dann hat D die Koordinaten D(2;-2:-1).

Answer 3

In der Schule werden Vierecke im Gegenuhrzeigersinn beschriftet. Vgl. z.B. http://www.mathe-lexikon.at/geometrie/ebene-figuren/vierecke/allgemeines-viereck/allgemein.html

D.h.

Nun mit einem Koordinatenursprung: