Thema: Analytische Untersuchung von Vierecken im dreidimensionalen Vektorraum
1. Weise nach, dassdie Punkte A (3/-1/2), B (1/0/-2), C (2/1/2), D (4/0/6) die Eckpunkte eines Parallelogramms bilden.
Deine Skizze/Zeichnung ist gut gelungen. Damit nicht alles übereinander liegt und die Skizze plastischer aussieht solltest du
1. Die Skala auf der x-Achse enger wählen
2. Hilfslinien, die zu den Punkten führen fein einzeichnen. (Genau die Linien, denen du (von der x-Achse aus gefolgt bist, bevor du den Punkt gesetzt hast)
AB=0B-0A= (-2,1,-4)
DC=0C-0D= (-2,1,-4)
Da AB = DC, bilden die Punkte ein Parallelogramm. qed.
2. Berechne die Seitenlängen dieses Parallelogramms sowie die Länge der beiden Diagonalen.
|AB| = √(4+1+16) = √21
BC= (1,1,4), |BC| = √(1+1+16) = √18
AC=(-1,2,0), |AC|=e= √(1+4) = √5
BD=(3,0,8), |BD|=f=√(9+64) = √73
3. Berechne die Koordinaten des Diagonalenschnittpunktes S.
0S= 0A + 0.5 AC = (3,-1,2) + (-0.5, 1, 0) = (2.5, 0, 2)
S(2.5 , 0, 2)
4. Wie lauten die Koordinaten der Eckpunkte des Vierecks, das man erhält, wenn das Parallelogramm an der x1-x3-Ebene spiegelt?
Die x2-Koordinate der Punkte ändert das Vorzeichen, während die x1- und x3-Koordinate fix bleibt.
A (3/-1/2), B (1/0/-2), C (2/1/2), D (4/0/6)
A'(3/1/2), B '(1/0/-2), C'(2/-1/2), D'(4/0/6)
5. Ergänze einen Punkt E, dass die Punkte ABDE ein Parallelogramm bilden.
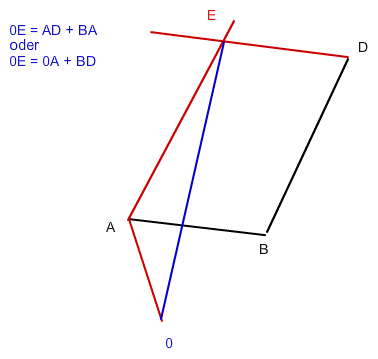
0E = 0A + BD = (3, -1, 2) + (3,0,8) = (6, -1,10)
E(6, -1,10)
6. Weise nach, dass es sich wirklich um ein Parallelogramm handelt.
Zu zeigen: AB = ED
ED = (4,0,6) - (6,-1,10) = (-2, 1, 4) vgl. mit AB oben. Stimmt. qed.
7. Betrachte das Viereck A (0/0/0), B (5/0/0), C (4/4/Wurzel aus 5), D (0/5/0). Weise nach, dass alle vier Seiten in diesem Viereck gleich lang sind und dass es sich trotzdem nicht um eine Raute handelt.
AB = (5, 0, 0) , | AB| = √25 = 5
AD = (0, 5, 0), |AD| = √25 =5
BC = (-1,4, √5), |BC| =√(1+16+5) = √22
CD = (-4, 1, √5), |CD| = √22
Die Behauptung ist somit falsch. Die 4 Seiten sind gar nicht gleich lang.