Wie errechne ich von einer parabelförmigen Brücke die Stützen?

Question

Es handelt sich um eine normale Brücke. Die Parabel ist unten geöffnet.
Die Höhe der Brücke beträgt 200m und die Spannweite 150m.
Die Stützen haben einen jeweiligen Abstand von 50m. Nun ist gefragt, welche Höhe
diese Stützen haben.

Nachtrag: Präzisierende Skizze: 

Druckfehler: Unten 150m Spannweite.

Comments

In deiner Skizze sollte die Spannweite gemäss Text 150 m sein. (?)

Nun haben deine Stützen in der Skizze aber den Abstand 50 m auch an beiden äusseren Teilen. Gäbe wieder 150m insgesamt.

---

Danke für die Fehlermeldung.

Das ist die richtige.     

Answer 1

 

entspricht die folgende Skizze Deiner Fragestellung?

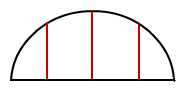
Dann ist die Aufgabe recht leicht zu lösen: 

Die Parabel hat die Form f(x) = ax² + b

In der Mitte der Brücke, die wir auf der y-Achse ansetzen, wird die Höhe berechnet durch: 

f(0) = a*0² + b = 200 => b = 200

Am rechten bzw. am linken Ende gilt:

f(-75) = (-75)² * a + b = 0 

f(75) = 75² * a + b = 0

75² * a = -200

a = -200/(75²) = -8/225

Also wird die Parabel beschrieben durch

f(x) = -8/225x + 200

Um die Höhe der Stützen zu berechnen, berechnen wir also: 

f(-75)

f(-25)

f(25)

f(75)

oder - falls eine Stütze sich genau in der Mitte der Brücke befindet:

f(0)

f(-50)

f(50)

Ich hoffe, ich konnte etwas helfen :-)

Besten Gruß

Comments

Ich habe es leider nicht besser gezeichnet bekommen.  
 

---

Das sieht ja schon ein wenig anders aus, die Berechnung verläuft aber ähnlich:

Wir haben nach wie vor
f(0) = 200

aber - wenn wir jetzt eine Spannweite von 200 (statt 150) Metern haben -
f(-100) = 0

und
f(100) = 0

(Falls die Spannweite doch 150 Meter sein sollte, bleibt es natürlich bei f(-75) = 0 und f(75) = 0)

Um die Länge der Stützen, die sich 50 Meter voneinander entfernt befinden, muss man dann, weil sich die Stützen ja oberhalb des Bogens befinden, rechnen:
Beispiel: Nehmen wir an, eine Stütze befindet sich bei x = 50, dann wäre die Länge der Stütze

200 - f(50)

Mach Dir das bitte anhand Deiner Skizze deutlich und versuch die Rechnungen einmal selbst.
Falls Du Rückfragen hast, meldest Du Dich einfach nochmal :-)

Answer 2

Ich modelliere die Brücke mit 

f(x) = -200/75^2·(50 - 75)^2 + 200

Skizze:

Also wäre die Länge der Stützen 

f(50) = f(100) = 177.78 m

Alternativ könnten wir Stützen bei 25, 75 und 100 m haben

f(25) = f(125) = 111.11 m

f(75) = 200 m

Comments

Die Brücke sieht aber komisch aus. Könnte es sein das die Spannweite eher 300 m ist ?

---

kann man also allgemein sagen das f(x)= Scheitelpunkt zum quadrat mal die quadrierte Differenz aus der Scheitelpunktsvertikalen  und der gesuchten vertikalen +max Höhe?