Nullstelle von f(x)= e^{3x}-9x

Question

Hallo an alle Matheüberflieger.

wie schon gesagt will ich die Nullstelle von f(x)= e^(3x)-9x berechnen. Also das gange =0 setzen.

Hier ist was ich habe.

e^3x-9x=0    /+9x

e^3x=9x   /ln

3x=ln(9x)

3x=ln(9)+ln(x)  /-ln(x)

3x-ln(x)=ln(9)

Jetzt hab ich alle x auf einer seite aber wie gehts weiter?

PS: das Ergebnis ist  x₁=0.206..... x₂=0.504 -- Aber wie?

Answer 1

Das geht wohl nur näherungsweise (Newtonverfahren oder so.).

Answer 2

Wie mathef auch schon geschrieben hat :

algebraisch ist dies nicht zu lösen.

Answer 3

Schon über 100 Jahre bekannt, selbst unter

https://de.wikipedia.org/wiki/Elementare_Funktion

zu finden: die LambertW-Funktion.

Dein Fall ist §5 unter

http://www.lamprechts.de/gerd/LambertW-Beispiele.html

mit a=3, b=9, c=0

Alle guten Rechner kennen sie

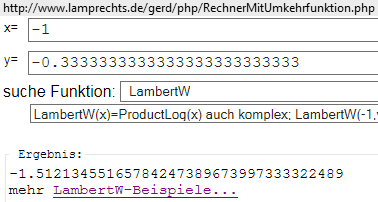
 -> hier 5 Lösungen in Tabellenform:

 n | x[n] =-LambertW(n, -0.3333333333333333333333333..)/3

-2 | 1.0636542453886575723414461 + 2.4830897289145333974998322 i

-1 | 0.5040448505526141579655800...

 0 | 0.2063537622453150373841089...

  1 | 1.0636542453886575723414461 - 2.4830897289145333974998322 i

  2 | 1.2546730939613966436930662 - 4.6240703464555534029320491 i

Probe:

f(x)=e^{3x}-9x ergibt für alle 5 Ergebnisse {also das x eingesetzt}  f(x)=0

Wenn Ihr keine komplexen Zahlen hattet, sind nur x[-1] und x[0] die reellen Lösungen.

Da unendlich viele Nachkommastellen, fehlt die gewünschte Genauigkeit in der Aufgabenstellung.

Answer 4

ich gehe von D = ℝ aus.

Die Gleichung kann man nicht explizit nach x auflösen.

f(x) = e^3x - 9x

f '(x) = 3·e^3x - 9

f "(x) = 9·e^3x

f "(x) > 0 für alle x∈ℝ  →  Graph von f  ist linksgegrümmt  →  G_f hat höchstens 2 Nullstellen

Diese kann man zum Beispiel mit dem Newtonverfahren ziemlich genau näherungsweise bestimmen:

Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben, findet man - auch mit einem einfachen Taschenrechner -  immer bessere Werte mit der Formel

x_neu =  x_alt - f(x_alt) / f ' (x_alt)

Startwert x = 0 :

x	f(x)	f '(x)
0	1	-6
0,166666667	0,148721271	-4,053836188
0,203353218	0,010362228	-3,478376421
0,20633226	7,37235E-05	-3,428807812
0,206353761	3,86344E-09	-3,428448438
0,206353762	0	-3,428448419

Starwert x =1 :

x	f(x)	f '(x)
1	11,08553692	51,25661077
0,783724738	3,444366617	22,49366778
0,630598683	0,955879924	10,8938042
0,5428534	0,210850851	6,289594365
0,509329641	0,024931875	4,826695926
0,504164228	0,000550528	4,614085746
0,504044914	2,9068E-07	4,60921354
0,504044851	8,17124E-14	4,609210965
0,504044851	0	4,609210965

Gruß Wolfgang