f(x) = a*x2 + bx + c
f '(x) = 2·a·x + b
f '(2) ist die Steigung an der Stelle x=2, diese soll 0 sein :
f '(2) = 4·a + b = 0 → b = - 4a [#]
A(1|4) liegt auf der Parabel :
f(1) = a + b + c = 4 → a - 4a + c = 4 → -3a + c = 4
B(4|7) liegt auf der Parabel:
f(4) = 16·a + 4·b + c = 7 → 16a - 16a + c = 7 → c = 7
c einsetzen:
-3a + 7 = 4 → -3a = -3 → a = 1 → b = - 4 (wegen #)
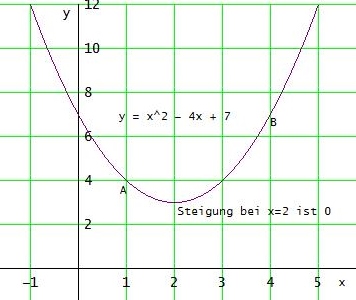
f(x) = x2 - 4x + 7
Gruß Wolfgang