Kreisbogen Länge berechnen

Question

und zwar habe ich ein Quadrat ABCD gegeben, in welches der Inkreis eingezeichnet wurde. 

Das Quadrat hat eine Seitenlänge von 28cm. 

Es wird nun ein zweites kleineres Quadrat Seitenlänge 7cm in das Quadrat einbeschrieben. (AB'C'D') die Seite

AB' liegt auf AB und AD' auf AD. 

Es geht nun darum die Länge des Kreisbogens des Inkreises, welcher sich innerhalb des kleineren Quadrates befindet zu berechnen.

Wie macht man das?

Answer 1

Erst mal eine Skizze:

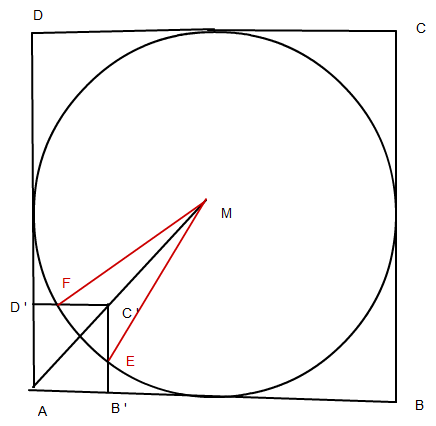
Jetzt  geht es ja nur darum den Winkel FME zu bestimmen.

Dazu kann man das Dreieck C ' M F betrachten, das hat bei C einen

Innenwinkel von 270° : 2 = 135° und es hat die Seite FM = Radius des Inkreises

= 14cm  und

C ' M =  halbe Diagonale des großen Quadrates minus

ganze Diagonale des kleinen Quadrates .

Dann kann man den Innenwinkel bei F über den Sin-Satz berechenund dann auch den Innenwinkel bei M über die Winkelsumme.

Comments

C ' M =  halbe Diagonale des großen Quadrates minus halbe Diagonale des kleinen Quadrates

Frage:

wie lässt sich das so herleiten?

---

Na ja: halbe Diagonale des großen geht von M bis A.

Dann das Stück von A bis C ' wieder abziehen,

bleibt C ' M übrig.

OHA, also nicht

" minus halbe Diagonale des kleinen Quadrates "

sondern

minus GANZE Diagonale des kleinen Quadrates .

Korrigiere ich oben auch !