Winkel in gleichseitig dreieckiger Pyramide ausrechnen

Question

EIne Pyramide mit gleichseitig dreieckiger grundfläche hat die Höhe h = 40 cm und die Grundseitenlänge a= 50 cm

ICh soll den Winkel zwischen a und einer Kante des Mantels berechnen +

den Winkel zwischen der Grundfläche und einer Seitenfläche

Bitte mit einer Skizze erklären

Answer 1

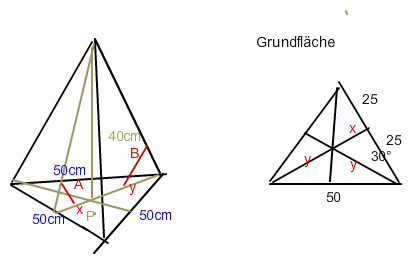
Grundfläche: Betrachte das kleine Dreieck mit dem 30°-Winkel

GK/AK = x/25 = tan 30°

x = 25*tan 30° =14.434

AK/HYP = 25/y = cos 30°

25/cos 30° = y = 28.868

Nun die beiden gesuchten Pyramidenwinkel in den rechtwinkligen Dreiecken:

A zwischen Seitenfläche und Grundfläche. 

GK/AK = 40/x = tan A

40/(25*tan 30°) = tan A

arctan (8/(5 * tan 30°)) = A = 87.52°

Nun zwischen Kante und Grundfläche:

GK/AK= 40/y = tan B

40/ (25/cos 30°) = tanB

arctan (8/5 * cos 30°) = B = 54.18°

Bitte sorgfältig nachrechnen, B müsste kleiner sein als A! Das stimmt schon mal. Allerdings scheint mir A etwas gar gross.

Comments

wie kommst du auf die 30°

---

da steht nirgeddwo ejne winkelangabe

---

Im gleichseitigen Dreieck messen alle Winkel 180*3 = 60°. Aus Symmetriegründen halbieren die Höhen die Winkel.

Mehr zu gleichseitigen Dreiecken hier: https://de.wikipedia.org/wiki/Gleichseitiges_Dreieck

---

kannst du es mir so erklären, dass die gegenkthete ankathe bei der formel ran kkmmr

---

Habe mit GK, AK, und HYP abgekürzt.

---

bei b ist doch der winkel falsch eingezeichnet oderr? der winkel muss doch zwischer einer kante des mantels sein

---

Richtig! Da darfst du noch ein wenig mehr ausrechnen.

Die Kantenlänge k bekommt man als
GK/HYP = h/k=  sin B
h* sinB = k = 40*sin  54.18°

nun noch die Höhe in der vorderen Mantelfläche einzeichnen. Der gesuchte Winkel C liegt rechts unten.

Es gilt AK/HYP = 25/k  = sin C = 25/(40*sin 54.18°)
C = arcsin (25/(40*sin 54.18°) ) = 50.42°

nachgerechnet mit:

https://www.wolframalpha.com/input/?i=+arcsin+%2825%2F%2840*sin+%28arctan+%288%2F5+*+cos+30°%29%29%29+%29

---

kannst du es in der Zeichnung auch ändern

---

Nein ich brauche ja das B in meiner Rechnung. Vielleicht finde ich die Zeichnung wieder und dann kann ich noch C einzeichnen.

---

 

Ich hab den Winkel so gezwichnet , aber ich habe was anderes raus : 59grad

---

Das sieht gut aus. Ist derselbe Winkel. Gut möglich, dass ich mich irgendwo verrechnet habe. Entweder kannst du jetzt deine Rechnung zur Kontrolle noch anfügen oder du suchst in meiner Rechnung den Fehler.