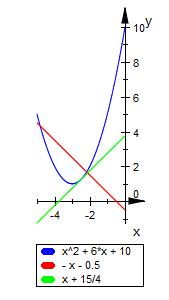
ich habe eine Gerade g1: y=-x-0,5 und eine
Parabel p1: y=x²+6x+10
meine Frage:
Wie ist die Gleichung einer Geraden, die
senkrehct zur ersten Gerade verläuft und Tangent
an die Parabel ist?
meine Idee ist erstmal dss die steigung
der Geraden 1 sein muss, damit m1 mit m2 -1 ergibt
m1 * m2 = -1
m1 = -1
m2 = -1 / ( -1 )
m2 = 1
p1 ( x ) = x ² + 6x +10
p1 ´ ( x ) = 2 * x + 6 = m2
2 * x + 6 = 1
x = -5/2
p1 ( -5 / 2 ) = (-5 / 2)^2 + 6 * ( -5 / 2 ) + 10 = 5 / 4
Berührpunkt
( -3 | 5 / 4 )
Tangente
5 / 4 = 1 * -3 + b
b = 15 / 4
t ( x ) = x + 15 / 4