Gerade aus dem Geradenbüschel bestimmen, die eine Tangente an die Parabel p ist

Question

Hallo liebe Gemeinschaft, 

Parabel mit der Funktionsgleichung p (x)  - 1/2 x²  +  3 x  - 1   und  Trägerpunkt  T  (3/6) eines Geradenbüschels. 

Bestimme die Gerade g aus dem Geradenbüschel, die eine Tangente an die Parabel p ist.

 

Ich denke, dass man zunächst die bei Funktionsgleichungen gleichsetzt. 

Aber wie und wo setze ich  T  ein?

 

Dankeschön für die Beiträge. 

Answer 1

T ist der Punkt durch den alle Geraden des Geradenbüschels laufen. Daher kann man die Geraden in der Punkt-Steigungsform wie folgt notieren:

ga(x) = a * (x - 3) + 6 = ax - 3a + 6

Nun setzt man p(x) = ga(x) und sucht das a für das es nur einen gemeinsamen Punkt gibt

-0.5x^2 + 3x - 1 = ax - 3a + 6
-0.5x^2 + (3 - a)x + (3a - 7) = 0

Diskriminante null setzen:

b^2 - 4ac = (3 - a)^2 - 4(-0.5)(3a - 7) = a^2 - 5 = 0

Es gibt nur eine Lösung falls: a = ±√5

g1(x) = √5 * (x - 3) + 6
g1(x) = -√5 * (x - 3) + 6

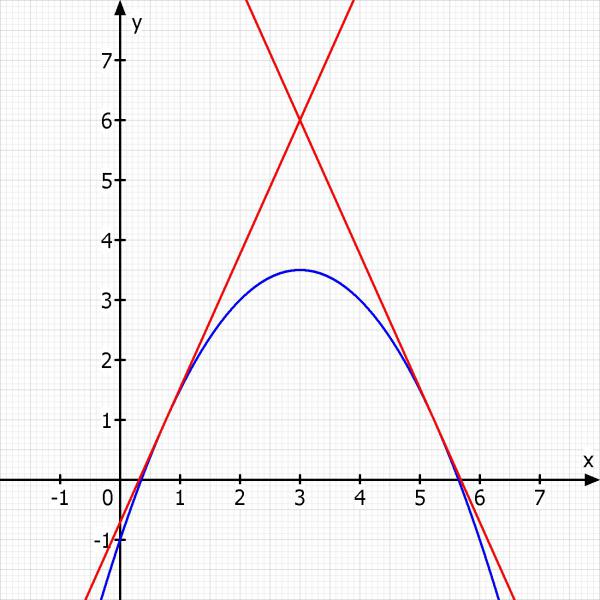
Skizze:

Answer 2

Parabel mit der Funktionsgleichung \(p (x) = - 0,5 x^2  +  3 x - 1\)  und Trägerpunkt \(T (\red{3}|\blue{6})\) eines Geradenbüschels.
Bestimme die Gerade g aus dem Geradenbüschel, die eine Tangente an die Parabel p ist.

\(p' (x) = - x +  3 \)

\( \frac{y-\blue{6}}{x-\red{3}}=- x +  3 \)

\(y=(-x+3)(x-3)+6 \)

Diese Parabel schneidet  \(p (x) = - 0,5 x^2  +  3 x - 1\) in den beiden Berührpunkten.

\( - 0,5 x^2  +  3 x - 1=(-x+3)(x-3)+6 \)

\(x_1≈0,76\)         \(y(x_1)=(-x_1+3)(x_1-3)+6=... \)

\(x_2≈5,23\)       \(y(x_2)=(-x_2+3)(x_2-3)+6=... \)

Nun noch die beiden Tangenten berechnen.