Für welches u wird das Volumen maximal?

Question

Aufgabe:

Für welches u wird das Volumen maximal?

\( f(x)=-\frac{1}{30} x^{5}+\frac{1}{2} x^{3} \)

Ein Punkt P (u/v) auf K mit 0<u<√15 bestimmt zusammen mit O(0/0) und Q(0/v) ein Dreieck OPQ. Durch Rotation dieses Dreiecks um die y-Achse entsteht ein Kegel. Für welches u wird das Volumen dieses Kegels maximal?

Die Kurve K schließt mit der positiven x-Achse eine Fläche A ein. A wird durch die Parallele zur y-Achse durch den Hochpunkt H von K in zwei Teile geteilt. Berechnen Sie die Inhalte der beiden Teilflächen. Eine Grade g durch H halbiert die Fläche A. An welcher Stelle schneidet g die x-Achse?

Comments

Genauer sind das ja zwei Aufgaben. Die erste ist doch nicht so wild. Nimm meine Skizze und zeichne dir durch den Hochpunkt eine parallele zur y-Achse.
Stelle des Hochpunktes über f'(x) = 0 ausrechnen und dann die beiden Teilflächen mit dem Integral berechnen.
Der zweite Teil ist etwas schwieriger. Auch da nimmst du die Skizze zeichnest eine Gerade durch den Hochpunkt und zeichnest die Gerade jetzt ungefähr so, dass man zwei gleiche Teilflächen hat. Dann überlegst du wie du die Linke Fläche ausrechnen kannst.
Dann stellst du den Term gleich der halben gesamten Fläche. Probier das zunächst alleine. Mach dir vor allem zum Verständnis eine Skizze. Die Funktion hast du ja bereits von mir als Skizze vorliegen.

Wenn du nicht weiter kommst, brauchst du keine neue Frage aufmachen, sondern schreibst ein Kommentar in die alte. Fragestellung ist dort ja auch vorhanden.

Also probier dich mal am Lösungsansatz.

Answer 1

Könnte es sein das das rotierende Dreieck einen Kegel beschreibt? ja, war ja sogar in der Aufgabe angegeben.

Wie lautet das Volumen vom Kegel? V = 1/3 * G *H

Wie bestimmen wir die Grundfläche G? G = pi * x^2

Wie bestimmen wir die Höhe H? H = f(x)

Also:

V = 1/3 * G * H = 1/3 * pi * x^2 * (1/2 * x^3 - 1/30 * x^5)
V = pi·x^5/6 - pi·x^7/90
V' = 5·pi·x^4/6 - 7·pi·x^6/90 = 0

x = 5·√21/7 = 3.273268353

f(5·√21/7) = 375·√21/343 = 5.010104622

Skizze:

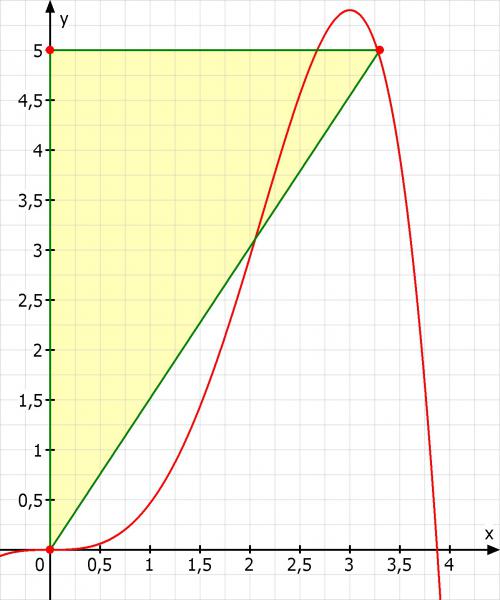
Nun probierst du aber den Rest mal alleine oder?