Monotonieverhalten der Funktion f mithilfe des Monotoniekriteriums bestimmen

Question

Aufgabe lautet:
Bestimmen Sie das Monotonieverhalten der Funktion f mithilfe des Monotoniekriteriums (siehe Bild) und skizzieren Sie anschließend den Graphen von f.
a) f(x)= (1/3)x^3-x b) f(x)= (1/3)x^3+x^2+x c) f(x)= (1/4)x^4-(1/3)x^3-x^2

Ich habe bei der a) jetzt 1 und -1 als Nullstellen => also 2 als Tiefpunkt und -2 als Hochpunkt. Dann habe ich daraus die Intervalle bestimmt ] -unedlich; -2[ streng monoton steigend, ] -2; 2 [ streng monoton fallend, ] 2; +unedlich [ . Bin mir aber nicht so sicher, ob das so bestimmt. Ich hab mich an der Seite de.serlo.org mit deren Thema "Monotonieverhalten berechnen" orientiert.

Und wie bitte schön skizziert man anschließend die Graphen von diesen komplizierten Funktionen? Wie geht man da vor? Wie geht man eigentlich bei dieser ganzen Aufgabe vor? Kann mir das jemand eventuell am Beispiel von a) verdeutlichen?

Answer 1

a) 

f(x) = 1/3·x^3 - x

f'(x) = x^2 - 1 = 0 --> x = -1 ∨ x = 1

f(-1) = 2/3 --> HP(-1 | 2/3)

f(1) = -2/3 --> TP(1 | -2/3)

Im Intervall ]-∞ ; -1] ist f(x) monoton steigend.

Im Intervall [-1 ; 1] ist f(x) monoton fallend.

Im Intervall [1 ; ∞[ ist f(x) monoton steigend.

Skizze

~plot~ 1/3*x^3 - x;{-1|2/3};{1|-2/3} ~plot~

Comments

Muss man nicht die 2te Ableitung bilden, die Nullstellen einsetzen, um so den x-Wert für ein Extrema zu bekommen? Den y-Wert bekommt man dann wiederum, indem man in die Ausgangsfunktion einsetzt.

---

Du kannst die hinreichende Bedingung für die Art des Extremums benutzen. Muss man aber nicht zwangsweise. Da ich bei dem Nullsetzen der ersten Ableitung zwei einfache Nullstellen bekomme sind es wirkliche Extrema. Also ein Hoch und ein Tiefpunkt. Der Hochpunkt hat dabei natürlich hier die höhere y-Koordinate. Der Tiefpunkt die niedrigere y-Koordinate.

---

Und wie kann man das, was wir jetzt berechnet haben, auf das Monotoniekriterium beziehen? Das verstehe ich nicht. Wie soll das Monotoniekriterium helfen bei dieser Aufgabe?

---

Ach so. Ich glaube, ich hab's. f'(x) ist ja die Steigung. Und die y-Werte die wir berechnen, stellen sozusagen die Steigungen dar. Und wenn z.B. f'(x)>gleich 0 ist, also der y-Wert auch >gleich 0 ist, so ist f(x) monoton steigend.

Stimmt das, wie ich das verstanden habe?

---

Vollkommen richtig.

---

Vielen, vielen Dank für die Hilfe!

Answer 2

Bestimmen Sie das Monotonieverhalten der
Funktion f mithilfe des Monotoniekriteriums

Das allgemeine Vorgehen ist

1.Ableitung bilden
Stellen mit waagerechter Tangente bestimmen
Wann ist die 1.Ableitung positiv ( steigend )
wann negativ  ( fallend )

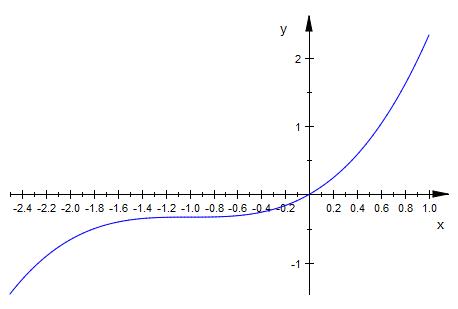
f(x)= (1/3)x³+x²+x

f ´( x ) = x^2 + 2 * x + 1

Stellen mit waagerechter Tangente bestimmen
x^2 + 2 * x + 1 = 0
x = -1

Wann ist die 1.Ableitung positiv ( steigend )
x^2 + 2 * x + 1 > 0
( x + 1 ) ^2 > 0
Stets, außer x = -1 dann 0.

Dies wäre monoton steigend nach den oben
aufgeführten Kriterien.

Dies ist zwar nicht gefordert aber man kann die
Art der " Stelle mit waagerechter Tangente "
noch bestimmen.

Ist der Verlauf der Steigung
steigend - null - fallend ist es ein Hochpunkt
fallend - null - steigend ist es ein Tiefpunkt

Bei
steigend - null - steigend
oder
fallend - null - fallend
ist es ein Sattelpunkt

Bei der Funktion ist es ein Sattelpunkt.

Comments

Test, Fülltext.Fülltext;

~plot~ 1/3 * x^{3} + x^{2} + x ~plot~