Hallo Sonnenschein,
Im Allgemeinen geht man davon aus, dass die Ecken so eines Parallelogramm in der Reihenfolge ABCD benannt werden. Dann ist \(CD=BA=A-B\) und \(D=C+CD=C+A-B\) also
$$D=\begin{pmatrix} 3 \\ -1 \end{pmatrix} + \begin{pmatrix} -2 \\ 2 \end{pmatrix} - \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \begin{pmatrix} -1 \\ -2 \end{pmatrix} $$
ein Bild sagt mehr als 1000 Worte:
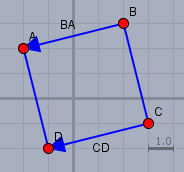
Diese Reihenfolge der Bezeichnung der Punkte ist aber nicht in Stein gemeißelt, also könnte man auch eine andere Reihenfolge wählen. Letztlich kommt es darauf an, welche von den drei Strecke \(AB\), \(BC\) und \(CA\) die Diagonale des Parallelogramms bildet. Eben hatten wir \(AC\) als Diagonale, daher verbleiben noch zwei andere Möglichkeiten:
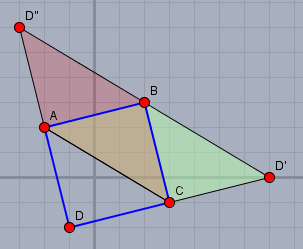
Beim Parallelogramm ACD'B ist \(BC\) die Diagonale und bei ACBD'' ist es \(AB\). Es gibt also in Summe drei Möglichkeiten.
zu c) Die allgemeine Regel ist: addiere die beiden Punkten, die sich gegenüberliegen sollen (die Diagonale) und ziehe den dritten Punkt davon ab. Warum ist das so?
Damit kann man die drei Punkte berechnen:
$$D= \begin{pmatrix} 4 \\ 2 \\ -1 \end{pmatrix} - \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \begin{pmatrix} -2 \\ 0 \\ 4 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$$
$$D\prime= -\begin{pmatrix} 4 \\ 2 \\ -1 \end{pmatrix} + \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \begin{pmatrix} -2 \\ 0 \\ 4 \end{pmatrix} = \begin{pmatrix} -5 \\ 0 \\ 8 \end{pmatrix}$$
$$D\prime\prime = \begin{pmatrix} 4 \\ 2 \\ -1 \end{pmatrix} + \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} - \begin{pmatrix} -2 \\ 0 \\ 4 \end{pmatrix} = \begin{pmatrix}7 \\ 4 \\ -2 \end{pmatrix}$$
klicke hier, dann siehst Du es in 3D.
Gruß Werner