von Graphen von f' und f'' auf f kommen?

Question

Ich hab als Graph die Funktion (x-1)^2+2 vorliegen, die f' ist. 
Und dann noch f'' als Graph, 2x-1
Die sind nur als Graphen gegeben, ich hab die Funktionen von denen hier selber aufgestellt.

Sie schneidet die x-Achse nicht, also kann f keine Extrema haben, oder?. Sie hat einen Tiefpunkt, also hat sie aber eine Wendestelle. Außerdem müsste Sie ja eine Funktion 3. Grades sein.

Comments

Verstehe ich das richtig, dass du eine Funktion dritten Grades angeben sollst, deren Ableitungen so sind, wie du sie angegeben hast? Allerdings muss f''(x) 2x - 2 sein.

---

Also die funktion wäre ja dann ein Polynom dritten Grades der Form f(x)1/3*x^3-x^2+x+c. Mit einem Wendepunkt bei x=1. Wie man jetzt auch c kommen soll ist mir auch ein Rätsel aus der 1. Ableitung erhält man auch keine weiteren Infos das nur komplexe Nullstellen. Dass heißt keine Nullstellen in R somit keine extrema. Heist bei dir als Graph als Funktionszeichnung?

---

ja stimmt, das sollte -2 sein

---

wie kommt man denn auf f, wenn es keine Extremstellen hat?

---

Zum Beispiel wenn eine Tangente in einem Punkt geben ist oder ähnliches. Mit den Informationen dir hier geben sind komme ich leider auf keine Lösung.

---

Ich kann doch den Term einer Funktion bestimmen, die keine Extremstellen hat. Wenn ich die Ableitungsfunktion habe, muss ich nur noch aufleten.

---

ja und wie willst du dann c bestimmen?

---

und noch eine frage: wie weiß man anhand der 1. Ableitung, ob es eine links rechts Wendestelle oder RL Wendestelle ist?

und wie weiß man, ob ein Sattelpunkt (Berührpunkt bei f' mit der x- Achse) steigt oder fällt, also wie zeichnet man es? da gilt ja f' und f'' = 0 und f''' ungleich 0

---

Also du untersucht ja mit der ersten Ableitung auf Extremstellen. Ist die zweite dann für das ermittelte x größer null -> Minimum kleiner null Maximum. Weißt du nun, dass es einen Wendepunkt hat. Hast du ja logischer weiße die Punkte für die Maxima/Minima und die Wendestelle/n. Bewegst du dich nun vom Minimum zur Wendestelle und die Funktion ist bis zur Wendestelle monoton wachsend liegt eine Linkskrümmung vor. Kommt nach der Wendestelle ein Maximum und die funktion ist weiterhin monoton wachsend liegt eine Rechtskrümmung vor. Wichtig bei der betrachtung ob etwas links oder rechts ist also das Monotonieverhalten. Wenn du dir das schlecht vorstellen kannst nimm einfach den x wert der Wendestelle und rechne dir ein paar Punkte links und rechts davon aus.

Answer 1

Hallo jc,

wenn man davon ausgeht, dass man nur die Graphen von f ' und f " (Gerade) hat, kann man nur feststellen, dass f

-   eine Polynomfunktion 3. Grades ist,

-   keine Extrempunkte und keinen Sattelpunkt hat (keine Nullstelle von f ')

-  eine Wendestelle bei x=1 (Nullstelle von f " mit Vorzeichenwechsel) hat

Man weiß außerdem, dass f - wie jede Polynomfunktion 3. Grades - symmetrisch zum Wendepunkt ist.

Der Graph kann etwa so aussehen, könnte aber auch beliebig nach unten oder oben verschoben sein:

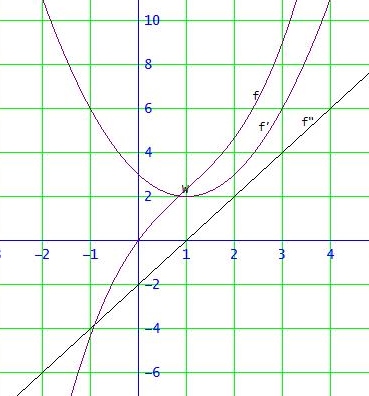
Wenn genügend Punkte der Geraden (f ") und/oder der Parabel (f ' ) eindeutig markiert sind, kann man natürlich auch deren Gleichungen bestimmen und f bis auf eine Integrationskonstante c durch Integration berechnen. Die Unklarheit bzgl. c ist der Grund dafür, das der Graph von f beliebig weit nach oben oder unten verschoben sein kann.

Gruß Wolfgang

Answer 2

Ausgehend von
f ´( x ) = ( x - 1 )² + 2

ist
f ´´( x ) = 2*x - 2

Die Stammfunktion von f ´( x ) ist
f ( x ) = ∫ ( x - 1 )² + 2 dx = ∫ x^2 - 2x + 3 dx
f ( x ) = x^3 / 3 - x^2  + 3x + c

Was hat das c zu bedeuten ?

Die Grafik zeigt dir die Funktion mit c = 1 und c = 4.
Durch ein anderes c wird die Funktion in Richting
y-Achse verschoben.
Die Steigung ( 1.Ableitung ) an jeder Stelle " x = "
ist jedoch dieselbe.
Mathematisch : das c entfällt beim Ableiten.

Beim Aufleiten gibt es unendlich viele mögliche
Funktionen. Dies wird durch das c ausgedrückt.

Alle Funktionen können im Rahmen einer
Kurvendiskussion auf Nullstellen,
Extrema usw untersucht werden

Bin bei Bedarf gern noch weiter behilflich.