Es gibt schon eine Formel, aber die sollte man sich selber überlegen können ...
Ich habe die Geraden in der XZ-Ebene mal gezeichnet. Mit ihren Aufpunkten \(P_g\) und \(P_h\) und ihren Richtungsvektoren \(r_g\) und \(r_h\).
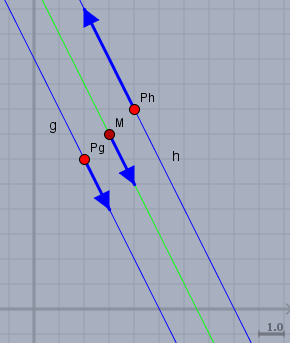
Zwei Geraden laufen parallel, wenn ihre Richtunsvektoren parallel - d.h. linear abhängig sind. Formal heißt das, es gibt eine Lösung für
$$r_h=t \cdot r_g$$
das ist hier für \(t=-0,5\) der Fall. Damit ist die Parallelität gezeigt.
Verschieden sind sie dann, wenn der Aufpunkt \( \) der jeweile anderen Gerade nicht auf der einen liegt. D.h. es gibt keine Lösung für
$$P_h = P_g + t \cdot r_g \quad \begin{pmatrix} 4\\ 7\\ 8 \end{pmatrix} = \begin{pmatrix} 2\\ 5\\6 \end{pmatrix} + t \cdot \begin{pmatrix}1 \\1 \\ -2 \end{pmatrix}$$
aus der ersten Zeile folgt \(t_x=2\) steht im Widerspruch zur dritten Zeile \(8 \ne 6 + 2 \cdot (-2)\). Damit ist gezeigt, dass die Geraden verschieden sind.
Eine Mittelgerade findet man, indem man von zwei beliebige(!) Punkte auf den Geraden den Mittelpunkt \(M\) bestimmt. Also am Einfachsten von den Aufpunkten \(P_g\) und \(P_h\). Es ist
$$M = \frac{1}{2}\left( P_g + P_h \right)$$
Und zusammen mit einem der beiden Richtungsvektoren ist die Mittelgerade \(m\) fertig. Welcher Richtungsvektor ist egal, da diese linear abhängig sind.
$$m: \space x = M + t \cdot r_h$$