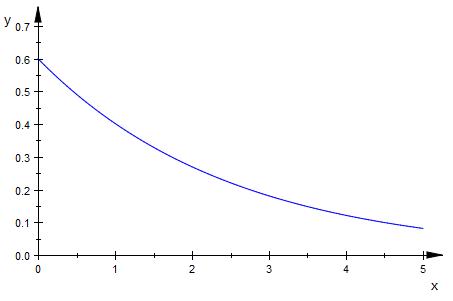
f ( x ) = 0.6 * e^{-0.4*x}
Eine e-Funktion ist stets > 0 und damit oberhalb
der x-Achse. Auch bei mal 0.6.
Damit ist die Fläche immer zwischen der Funktion
und der x-Achse.
 Eine e-Funktion hat als Stammfunktion stets eine
Eine e-Funktion hat als Stammfunktion stets eine
e-Funktion.
Ich leite probeweise einmal ab
( e^{-0.4*x} ) ´ = e^{-0.4+x} * (-0.4)
Sieht schon ganz gut aus. Wir wollen als Faktor
allerdings 0.6.
-0.4 * x = 0.6
x = -1.5
Stammfunktion
-1.5 * e^{-0.4*x} abgeleitet ergibt 0.6 * e^{-0.4*x}
[ -1.5 * e^{-0.4*x} ] zwischen 0 bis 5
-1.5 * [ e^{-0.4*5} - e^{-0.4*0 } ]
1.297
mfg Georg