Mmh, ich bin leider schon so lange raus, aber ist Volumenberechnung, vereinfacht, nicht
V= L * B * H?
Das neue Volumen würde man dann doch
V= (L * 1,1) * (B * 1,1) * H oder
V= (L * (1 + P) * (B * (1 + P)) * H rechnen?
Aber das ist sicherlich dasselbe wie bei Georgborn?? *lach*
Was meint ihr, sollte man hier, man hat ja keine Werte, sich eine Tafel Schokolade nehmen und diese Werte verwenden?
Die grafische Darstellung haben wir jetzt als Zuwachs Volumen/Fläche dargestellt, aber da sind wir wohl mal noch völlig daneben.
Die Funktionsgleichung soll ja in Normalform (V= (L * 1,1) * (B * 1,1) * H) als auch Scheitelpunktform geschrieben werden. Wenn wir nur eine "lineare" Gleichung haben, dann haben wir ja keinen Scheitelpunkt?
Ein Tipp gab uns der Lehrer, verwendet eine Wertetabelle, da bin ich schon wieder raus... Ach ist das mist, wenn man so lange aus der Schule raus ist :-/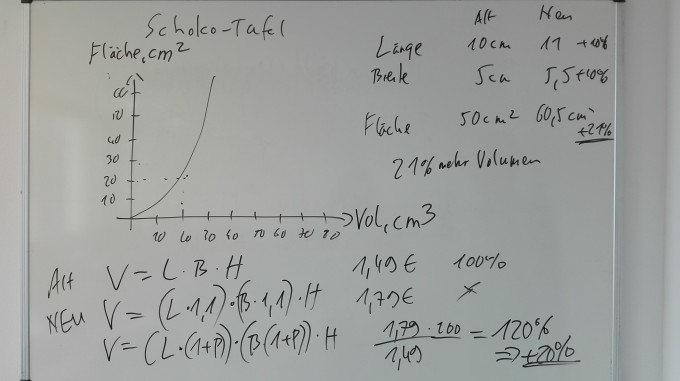
Ich hänge mal mit an, was wir eben mal kurz erprobt haben :-)
Ein riiiiesen Dank auf jeden Fall schon mal