Wahrscheinlichkeiten unabhängiger Ereignisse

Question

Von zwei unabhängigen Ereignissen sind die folgenden Ergebnisse bekannt:
P(A ∩ B) = 2/5 und P(B \ A) = 1/5
Berechnen Sie die folgenden Wahrscheinlichkeiten und geben Sie dabei vollständig gekürzte
Brüche an.
Hinweis: Aus den gegebenen Informationen lässt sich zunächst P(B) berechnen!

Comments

also meine frage ist wie ermittel ich P(B)

Answer 1

 

Du könntest zum Einen eine Vierfeldertafel benutzen:

                        A            Nicht A

B                    2/5            1/5               3/5

Nicht B          4/15          2/15            2/5

                       2/3            1/3                 1

Die roten Werte waren gegeben, die restlichen Zahlen lassen sich einfach berechnen: Am Rande müssen immer die Summen der jeweiligen Spalten bzw. Zeilen stehen, und diese müssen wiederum 1 ergeben. 

Die Felder in der Mitte müssen bei voneinander unabhängigen Ereignissen das Produkt der jeweiligen äußeren Summen sein, also z.B. 3/5 * 2/3 = 2/5 oder 2/5 * 2/3 = 4/15

Oder Du machst Dir ein kleines Venn-Diagramm: 

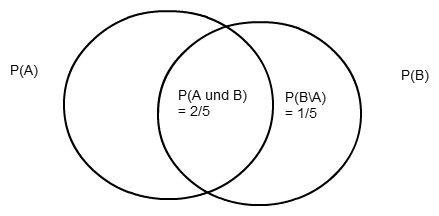
Auch hier siehst Du sofort, dass P(B) = P(A und B) + P(B\A) = 3/5 ist.

Oder Du nutzt ganz einfach die von Unknown angegebene Formel :-)

Besten Gruß

Comments

Ich Daume Dich mal hoch :).

Viel schöner/ausführlicher als das meinige. Hab Dank.

---

@ Unknown:

  Ich bin auf so etwas angewiesen, weil ich mir Formeln so schlecht merken kann :-)

Answer 2

Hi,

P(B) ergibt sich aus folgender Beziehung:

P(B) = P(A ∩ B) + P(B \ A) = 2/5 + 1/5 = 3/5


Grüße