Warum haben die Funktionen an zwei Stellen die selbe Ableitung?

Question

die Aufgabe lautet: Gibt es für die Funktionen f mit f(x) = x² + 3;  g mit g(x) = x³ und h mit h(x) = 2x + 6 jeweils eine Stelle mit der gleichen Ableitung?

f und g sollen an den Stellen x= 0 und x= 2/3 die gleiche Ableitung haben. Aber warum hat es zwei x Stellen? Man muss doch die beiden gleichsetzen -> 2x = 3x² => x= 2/3 woher kommt die Null?

Answer 1

2x = 3x² 

2x-3x² = 0

x(2-3x) = 0

Mit dem Satz vom Nullprodukt folgt: x = 0 oder 2-3x = 0 und damit haben wir dann: x₁ = 0 und x₂ = 2/3

Wenn du einfach durch x teilst in der Ausgangsgleichung verlierst du eine Lösung.

Answer 2

f = x² + 3;  g mit g(x) = x³
jeweils eine Stelle mit der gleichen Ableitung?

besser

jeweils eine Stelle mit der gleichen Steigung oder
Ableitungswert ?

f ´( x ) = g ´( x )
2 * x = 3 * x^2
3 * x^2 - 2 * x = 0
x * ( 3 * x - 2 ) = 0
x = 0
3 * x - 2 = 0
x = 2 / 3

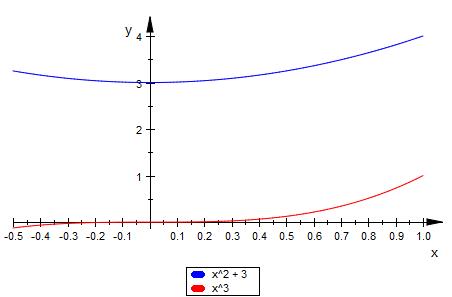
Wenn ich je eine Tangente bei x = 2/3 an die Kurven
einzeichne sind die Tangenten parallel weil sie die
gleiche Steigung haben.
Für x = 0 ebenso.