Aufgabe aus der Musterlösung des Profs: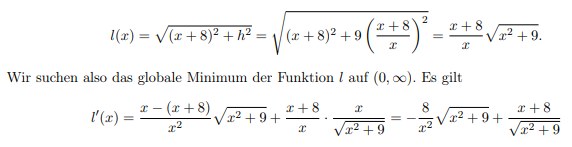
Text erkannt:
\( l(x)=\sqrt{(x+8)^{2}+h^{2}}=\sqrt{(x+8)^{2}+9\left(\frac{x+8}{x}\right)^{2}}=\frac{x+8}{x} \sqrt{x^{2}+9} \)
Wir suchen also das globale Minimum der Funktion \( l \) auf \( (0, \infty) \). Es gilt
\( l^{\prime}(x)=\frac{x-(x+8)}{x^{2}} \sqrt{x^{2}+9}+\frac{x+8}{x} \cdot \frac{x}{\sqrt{x^{2}+9}}=-\frac{8}{x^{2}} \sqrt{x^{2}+9}+\frac{x+8}{\sqrt{x^{2}+9}} \)
l(x) ableiten.
Unklar: Auf das Ergebnis der Ableitung kommen.
Edit: nur g'(x) scheint unklar zu sein. Hier benutzt man ja die faktorregel
Lösungsansatz:
Edit nach dem erstellen des Posts: Ich habe vermutlich g oder g' falsch bestimmt. der Rest scheint übereinzustimmen. Hier der ganze Ansatz:
$$ \frac{x+8}{x} \sqrt{x^{2}+9}= l\\ l\rarr l' = f'g + fg' \\ f= \frac{x+8}{x} =\frac{ff}{fg} \rarr QR \rarr ff= x+8 \rarr ff' = 1 \ und \ fg =x\rarr fg'=1 \\ f'=\frac{ff'fg-fffg'}{fg^2} = \frac{1(x)-(x+8)}{x^2}=-8/x^2 \\ g=(x^2+3^2)^{1/2}\rarr PO_{tenzregel}\rarr \frac{1}{2}(x^2+3^2)^{\frac{1}{2}-1} = \frac{1}{2(x^2+3^2)^{1/2}} =g' \\ l'= \frac{-8}{x^2}\sqrt{x^2+3^2}+\frac{x+8}{x} \cdot \frac{1}{2\sqrt{x^2+3^2}}$$