Satz des Pythagoras: Berechne die Länge des Seiles

Question

15. Figur 2 zeigt die Giebelseite des Daches eines älteren Hauses, Berechne die Längen \( x \) und \( y \).

16. In einem Glockenturm hängt das Seil zum Läuten der Glocke. Wenn man das Ende des Seils um \( 2 \mathrm{m} \) seitlich aus der Ruhelage bewegt, so hebt sich das Seilende dabei um 10 cm (Figur 4). Berechne die Länge des gespannten Seils.

Answer 1

15. Hätte ich jetzt persönlich über ein Gleichungssystem gelöst

x·COS(60°) + y·SIN(60°) = 5.4
x/2 + √3·y/2 = 27/5

x·SIN(60°) + y·COS(60°) = 4.8
√3·x/2 + y/2 = 24/5

Die Lösung lautet dann: x = 2.913843876 ∧ y = 4.553074360

16.

(x - 0.1)^2 + 2^2 = x^2
x^2 - 0.2·x + 4.01 = x^2
-0.2·x + 4.01 = 0
x = 4.01/0.2 = 20.05 m

Oh. Kann das Seil wirklich so lang sein?

Comments

Sehr schön. Nur gehe ich erst in die 9. Klasse und kann dort nicht mit diesem Rechenweg ankommen, weil wir COS und SIN noch nicht haben. Außerdem kann ich die Rechnung nicht ganz nachvollziehen: Den ersten Schritt bei Nr. 16 habe ich auch so nur ist 2^2 doch nicht 4,01. Und warum ist links dann auch 0,2*x statt 0,1*x? Das Ergebnis bei Nr. 16 kann aber gut hinkommen. Die Figur 4 hat ein ähnliches Längenverhältnis.

---

Achtung

(x - 0.1)² + 2² = x²

Hier ist eine binomische Formel

(x - 0.1)^2 = x^2 - 0.2x + 0.01

Auflösung sollte stimmen. Bei 16 hab ich ein Problem denn ich muss den Winkel ja irgendwie mit einbeziehen. Wenn der 70 Grad wäre würde das ja anders aussehen.

Also müsstet ihr eigentlich etwas zu Winkeln angesprochen haben in rechtwinkligen Dreiecken.

---

Man kann das auch ohne Sinus und Kosinus probieren. Habe gerade ein wenig rumexperimentiert, ist mir jetzt aber zuviel zum Schreiben/Zeichnen.

Grundgedanke: Verlängere die Seiten x (auf beiden Seiten). Dies bildet ein gleichseitiges Dreieck (da wir 60°-Winkel haben). Zusätzlich noch eine Parallele zur Grundseite in Höhe der Schnittpunkte x-y und man kann eigentlich alles berechnen, wenn ich mich nicht verzettelt habe. Pythagoras braucht es, sin/cos etc nicht ;).

Grüße


P.S.: Die 20,05 m kann ich bestätigen ;).

---

Ah noch einfacher ist es einfacher ist es Deinen Weg zu gehen, Mathecoach, wobei statt sin und cos einfach vorausgesetzt wird, wie die Formel für die Höhe eines gleichseitigen Dreiecks lautet:

Das blaue ist jeweils die Höhe im gleichseitigen Dreieck ;).

---

Ja, ich habe die binom. Formel übersehen. Danke.

---

So, Nr. 16 habe ich jetzt vollständig geblickt. Bei Nr. 15 habe ich irgendwie immer 2 Unbekannte. Kann jemand mir bitte nochmal einen Rechenansatz schreiben?

---

Mein Ansatz ist schon richtig. Nimm aber nur jeweils die zweite Zeile.

Zunächst leitest du dir die Seitenlängen in einem Dreieck her, wo die Winkel 30, 60 und 90 Grad sind.

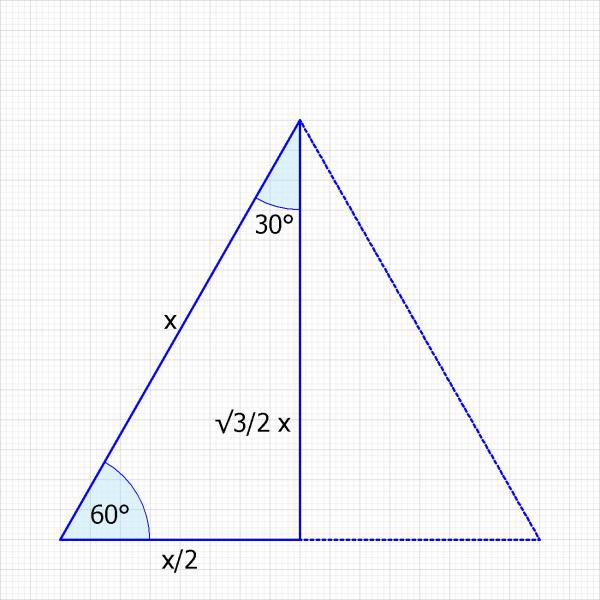
Dazu teilst du das ein gleichseitiges Dreieck über die Höhe in zwei kongruente Dreiecke. Jetzt fragt man wie groß die Seiten sind wenn vorher eine Seite x lang war.

Da sie kongruent sind ist die untere Seite sicher x/2

Für die Höhe gilt

h^2 = x^2 - (x/2)^2
h^2 = x^2 - x^2/4
h^2 = 3/4*x^2
h = √3/2*x

Nun verwendest du einfach die zweiten Zeilen meiner Gleichungen, bei denen ich jeweils die Hälfte und √3/2 der entsprechenden Länge benutze.

---

Wie kommt man von h^2 = x^2-x^2/2 auf h^2 = 3/4*x^2 ??? Auf die 4.8 komme ich aber ist das nicht schon y?

---

Dort steht 

h² = x² - (x/2)² 

Ich multipliziere die hintere Klammer einfach aus. Zähler mal Zähler und Nenner mal Nenner

h² = x² - x²/4 

Nun fassen wir zusammen 

a - a/4 = a - 1/4 a = 3/4 a

h² = 3/4*x² 

Oben in meiner Lösung stehen die Werte die eigentlich heraus kommen sollten. Soweit ich mich nicht verrechnet habe.

---

Also:

y²  = (√3/2*x)² * 2,4²

y² = (√3/2*4,8)² * 5,76

y² =  4,8²

Irgendwie ist mir alles weitere unklar...

---

Der Ansatz zur Berechnung von x und y bleibt aus meiner ersten Rechnung

1/2·x + √3/2·y = 5.4
√3/2·x + 1/2·y = 4.8

Die obige Rechnung diente nur dafür die Faktoren 1/2 und √3/2 vor x und y jeweils herzuleiten wenn man den sin/cos noch nicht gehabt hat.

Du rechnest also mit dem obigen Gleichungssystem aus 2 Gleichungen mit 2 Unbekannten.