Kurvendiskussion: Periodizität bestimmen

Question

Ich muss bei der folgenden Funktion die Periodizität bestimmen, habe mir Texte dazu durchgelesen und Videos angesehen, verstehe, was die Periodizität ist, habe aber keine Ahnung, wie man das rechnerisch bestimmt.

Ich hoffe, dass mir jemand helfen kann!

f(x)= 1-2*sin(1-2x)

Answer 1

Hallo ih,

> .... bei der folgenden Funktion die Periodizität bestimmen

f(x) = 1-2*sin(1-2x)

y = a * sin(bx + c) + d   hat die Periode  2π / |b|

bei dir:  a = - 2  ,  b = - 2  ,  c = 1  ,  d = 1

bei dir also Periode = 2π / 2 = π

Gruß Wolfgang

Comments

Jetzt hab ich das verstanden Als weiteren Punkt muss ich hier die Nullstellen (es gibt nur 2?) rausfinden: Muss ich dabei die ganze Funktion hernehmen, sprich 1-2*sin(1-2x) oder nur sin(1-2x) ?

Tausend Dank!

---

du musst f(x) = 0 setzen

1-2*sin(1-2x) = 0   | + 2*sin(1-2x)  | ↔ 

2*sin(1-2x) = 1     | : 2

sin(1-2x) = 1/2   

ergibt  1 - 2x = π/6 , also x = 1/2 - π/12 als Nullstelle

weitere Nullstellen ergeben sich aus:

1 - 2x  =  π/6 + k * π     mit k∈ℤ  

.....

Answer 2

(x)= 1-2*sin(1-2x)

Die 1 verschiebt die Kurve nur nach oben
Die ( 2 * ) sorgt für eine 2-fache Amplitude.

Wichtig ist nur die reine
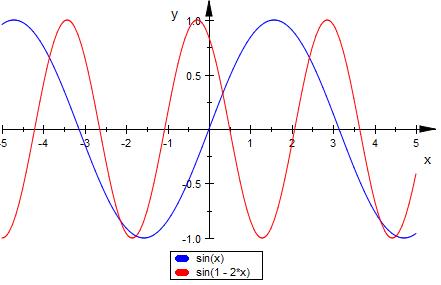
sin ( 1 - 2x )
Funktion

Nullstellen der sin Funktion
sin ( 0 ) = 0
sin ( π ) = 0
sin ( 2 * π ) = 0

Wobei zwischen
sin ( 0 ) = 0
sin ( 2 * π ) = 0
eine Periodenlänge ist

Was sind die Nullstellen von sin ( 1 - 2x )
sin ( 1 - 2x ) = sin ( 0 )  | arcsin
1 - 2x = 0
2x = 1
x = 0.5

sin ( 1 - 2x ) = sin ( 2 * π )  | arcsin
1 -2x = 2 * π
2x = 1 - 2 * π
x = 1/ 2 - π

Periodenlänge von sin ( 1 - 2x )
0.5 - ( 1/2 - π )
π

1.Nullpunkt = 0.5
weiterer Nullpunkt nach rechts 0.5 + π = 3.64
weiterer Nullpunkt nach links 0.5 - π = -2.64

Es sind auch andere, kürzere Antworten möglich.

Comments

Ich habe ehrlich gesagt nicht ganz verstanden, wo Du da die Periodizität ausrechnest. Braucht man dazu die Nullstellen? Geht das auch schneller auszurechnen? Ich würde das schon selbst machen, jedoch verstehe ich absolut gar nichts.

---

Periodizität heißt doch :
wann oder in welchem Abstand wiederholt sich
die Funktion.

Man prinzipiell jeden beliebigen Punkt
wählen und dann schauen wann kommt der
Funktionswert wieder vor.

Bei der sin-Funktion bietet sich an
- die Nullstellen
- das Maximum
oder
- das Minimum

---

Ach so, und Du hast dazu die Nullstelle bestimmt: Das bedeutet die Antwort auf die Periodizität ist somit 0,5 oder habe ich etwas falsch verstanden? DANKE!!!

---

Nein. Die Periode ist π.

Das ist immer der Abstand von der ersten zur dritten Nullstelle.

s. Grafik oben.

---

Ach so, danke, ich habe nur noch eine Frage: In dieser Funktion gibt es drei Nullstellen, die sich aber nur Pi immer wieder wiederholen, ist das richtig? Und wenn ich nun die Nullstelle der ganzen Funktion herausfinden möchte, dann brauche ich aber den ganzen Ausdruch (1-2*sin(1-2x)) und nicht nur sin(1-2x). Stimmt das so auch?

Damit wäre mir sehr geholfen! Danke an alle!!

---

1. Frage: Ja
2. Frage: Für die realen Nullstellen brauchst du den ganzen Ausdruck, ja.
Da aber die 1 und die 2 vor dem Sinus keine Streckung oder Stauchung entlang der x-Achse bewirken, kannst du für die Periode auch den Sinusterm  alleine nehmen, wie oben von Georg gemacht.

---

Hallo kati,

im direkten Unterricht kann dein Lehrer dir
die Sachverhalte sicherlich besser erklären als
es über das Internet möglich ist.

Du mußt dir nur merken

Allgemeine Form einer sinus-Funktion
f ( x ) = a + b * sin ( c * x + d )
hat dieselbe Periodenlänge wie
g ( x ) = sin ( c * x )

Bis auf den Faktor bei x kann alles fortfallen.

Nullstellen
sin ( 0 ) = 0
sin ( 2π ) = 0 ( volle Periodenlänge )

Wenn der Term in der Klammer 0 oder
2π ist dann ist der sinus eine Nullstelle.

g ( x ) = sin ( c * x )
c * x = 0   => x1 = 0 ( gilt für jedes c )
c * x = 2π  => x2 = 2π / c
Periodenlänge
x2 - x1 = x2 - 0 = x2

für dein Beispiel gilt
f ( x ) = 1 - 2 * sin ( 1 - 2x )
reduziert zu
g ( x ) = sin ( -2x )
x2 =  2π / c = 2π / -2
x2 = -π

Sollte ein negativer Betrag herauskommen
dann positiv setzen
Periodenlänge = π

Also was ist die Periodenlänge von

f ( x ) = -5555 - 4 * sin ( 4.567 * x + 23.1 ) ?

Zur Kontrolle
2π / 4.567 = 1.376